A Study of Slanted-Edge MTF Stability and Repeatability

by Jackson K.M. Roland

Abstract

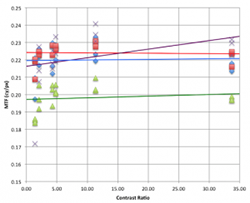
The slanted-edge method of measuring the spatial frequency response (SFR) as an approximation of the modulation transfer function (MTF) has become a well known and widely used image quality testing method over the last 10 years. This method has been adopted by multiple international standards including ISO and IEEE. Nearly every commercially available image quality testing software includes the slanted-edge method and there are numerous open-source algorithms available. This method is one of the most important image quality algorithms in use today. This paper explores test conditions and the impacts they have on the stability and precision of the slanted-edge method as well as details of the algorithm itself.Real world and simulated data are used to validate the characteristics of the algorithm. Details of the target such as edge angle and contrast ratio are tested to determine the impact on measurement under various conditions. The original algorithm defines a near vertical edge so that errors introduced are minor but the theory behind the algorithm requires a perfectly vertical edge. A correction factor is introduced as a way to compensate for this problem. Contrast ratio is shown to have no impact on results in an absence of noise.

Correction 2021-09-24 (thanks to Kenichiro Masaoka) :

Download the study