|
|
The basic premise of this work is that Information capacity is a superior metric It is better than sharpness or noise, which it incorporates, and it can be used To test the premise under a variety of conditions, we use the Image Processing module |
|
Related pages Image Information Metrics: Information Capacity and more contains key links to documentation, white papers, news, and more on image information metrics. The paper from Electronic Imaging 2024, Image information metrics from slanted edges, contains the most complete exposition of the image information metrics. The material is also covered in various levels of detail in the three white papers linked from Image Information Metrics.
Information capacity measurements from Slanted edges: Equations and Algorithms contains the theory. Image information metrics from Slanted edges: Instructions contains the instructions for performing the calculations. The slanted-edge method, which is faster, more convenient, and better for measuring the total information capacity of an image, is recommended for most applications, but the Siemens star method (2020) is better for observing the effects of image processing artifacts (demosaicing, data compression, etc.). |
Why simulate image processing? – Applying image processing
Why simulate image processing?Image processing (ISP) can affect several key performance indicators, especially object and edge detection metrics, SNRi and Edge Location σ (derived from Edge SNRi). There are a number of practical questions that can be addressed through simulation. These include,
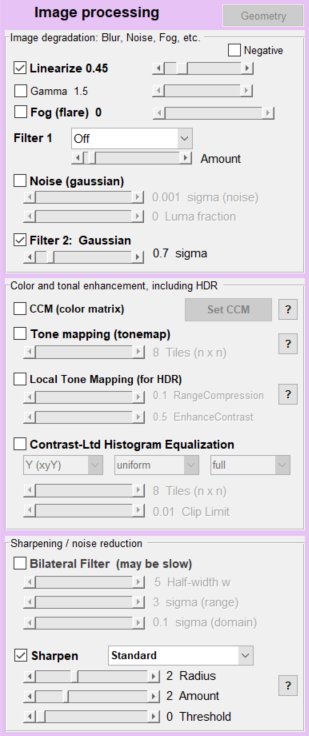
We know from experience that bilateral filters, which are nether linear nor uniform, tend to improve human perception of image quality, but they also increase measured information capacity while removing information from the image. Therefore we are most interested in uniform, linear image processing. Image processing can be simulated with the Imatest Image Processing module. Controls are shown on the right. The functions of greatest importance for analyzing machine vision performance are Linearize, Filter 2: Gaussian (similar to Filter 1), and Sharpen — Standard, which are shown checked. |
|
Nonlinear functions should be avoided because they do not give reliable results. These include Tone mapping, Tone Mapping, Contrast-Ltd Histogram Equalization, and Bilateral Filtering. In the process of writing the EI2024 paper, we discovered that USM (Unsharp Masking) sharpening is not linear. There was no indication of this in the MATLAB documentation. This changed the Noise Equivalent Quanta measurement, which should be unaffected by linear processing. We discuss USM nonlinearity in the Image Processing page and in Interpolated slanted-edge SFR (MTF) calculation. |
Applying image processing
We are most interested in the combined effects of lowpass filtering and sharpening.
To apply image processing to an image file,
- Open Image Processing. The window shown below appears. Image Processing instructions contains more detail.
 Image Processing opening window
Image Processing opening window
- Read the file by pressing .
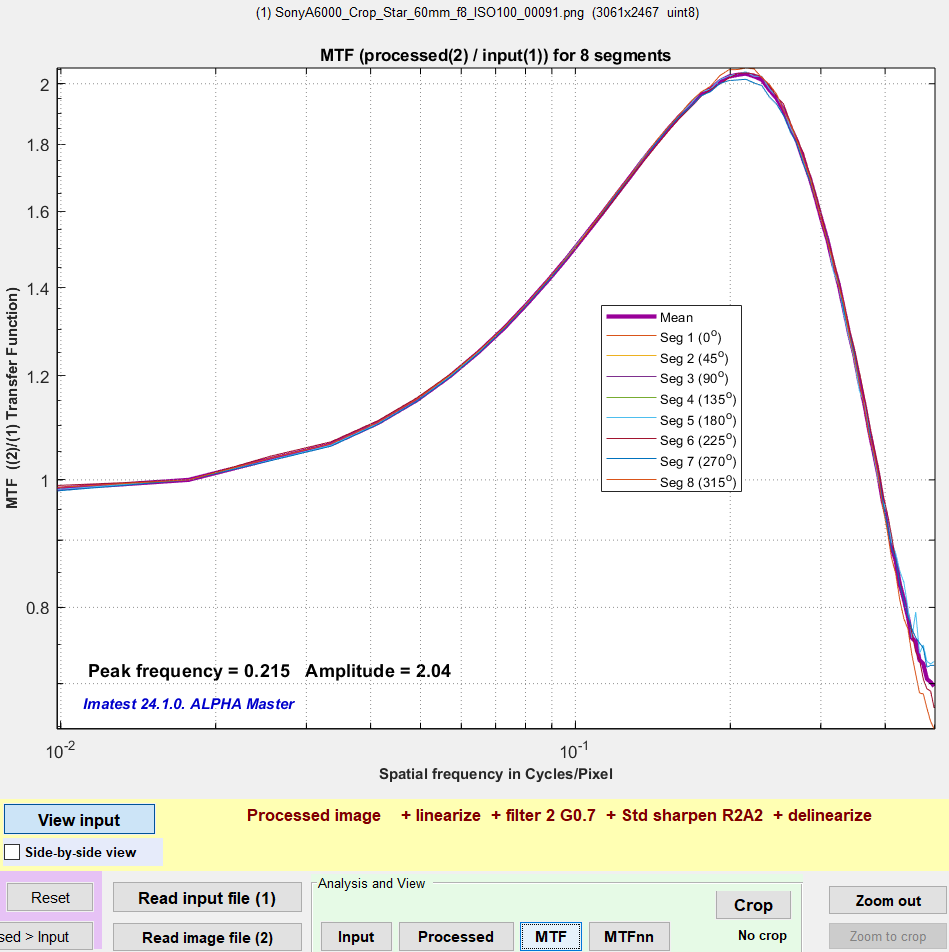
- Set the image processing. A typical example is shown above. Linearize, Filter 2, and Sharpen are checked. The file will be linearized assuming an encoding gamma of 0.45, blurred with a gaussian filter with σ = 0.7 pixels, sharpened (standard) with R = 2, A = 2, then re-gamma-encoded to gamma = 0.45.
- Press . Details on viewing the results are in the Image Processing instructions. We show a small version of the transfer function (MTF) on the right. Click on it to view full-sized.
- To save the processed file, press .
In running several images, starting with a reasonably sharp raw-converted image, we found that moderate lowpass filtering (LPF), helped; LPF with moderate sharpening gave similar results (but could be less susceptible to interference from neighbors), but strong sharpening without LPF degraded the Edge SNRi.
Results
Quick summary of results: the mildly sharpened + LPF result is similar to the filtered result. But the strongly sharpened result shows some degradation (about 2dB). Click on the images to view full-sized.
| Unprocessed (no ISP) |
 |
Lowpass-filtered (LPF) σ=0.7 Slight improvement |
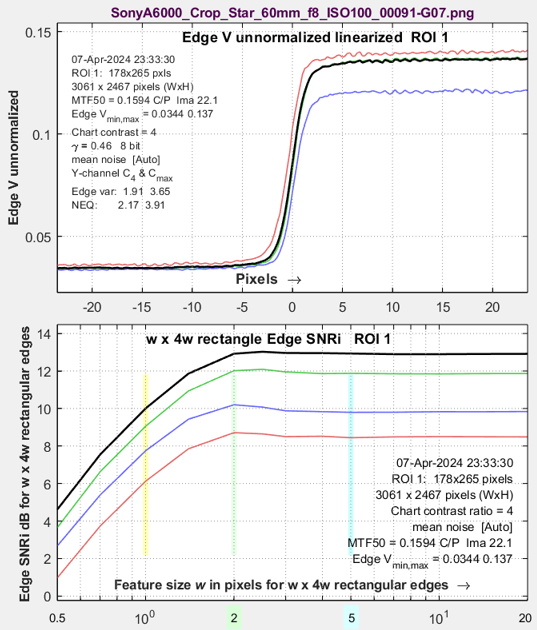 |
| Sharpened + LPF R=2 A=1 σ=0.7 |
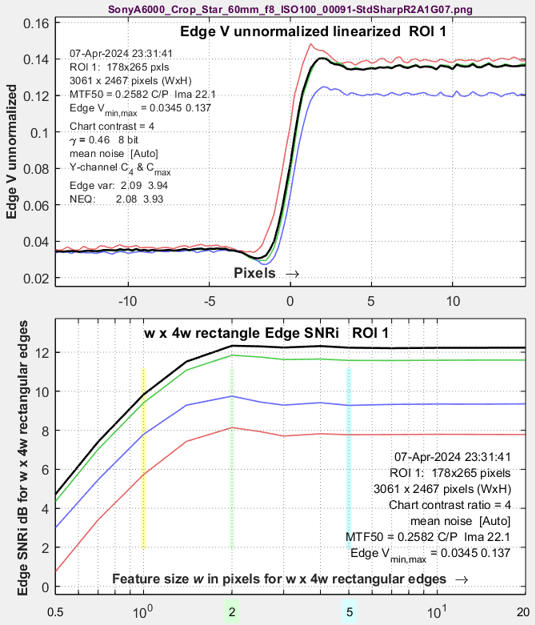 |
Strongly sharpened R=2 A=3 Definite degradation |
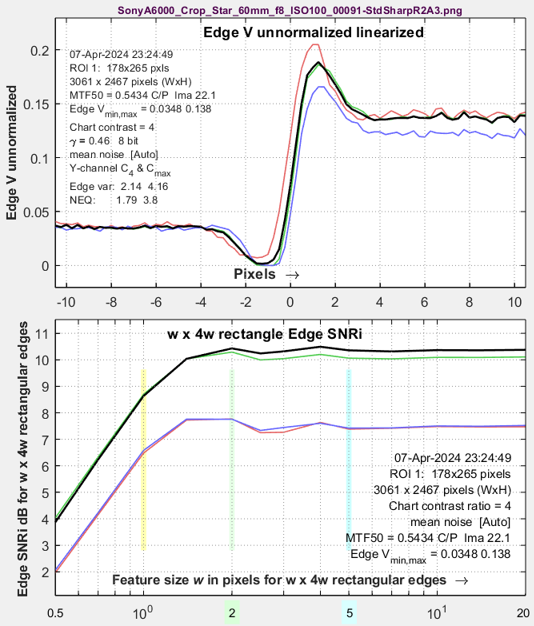 |
Appendix: The problem with Unsharp Mask (USM)
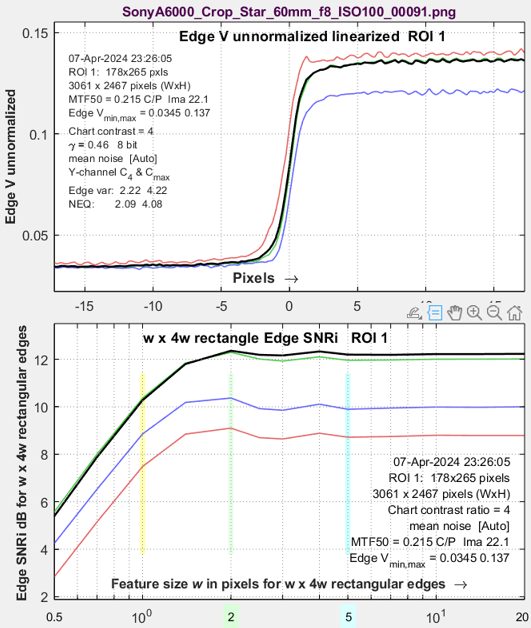
According to the theory presented in the Electronic Imaging 2024 paper, linear, uniform, and reversible image processing should have an identical effect on SFR2(f) and NPS(f), where NPS(f) is the Noise Power Spectrum, and hence should not affect Noise Equivalent Quanta, \(NEQ(f)=\mu\ SFR^2(f) / NPS(f)=\mu\ K(f)\), where “reversible” means no response nulls below the Nyquist frequency (0.5 C/P). But we found inconsistencies in NEQ(f) when we applied Unsharp Mask (USM) sharpening (the MATLAB imsharpen function). We expected imsharpen to be linear, but we eventually found out that it was not. The nonlinearity is omitted in the MATLAB documentation.
Results for an unprocessed image and images processed with USM and linear sharpening are shown below.
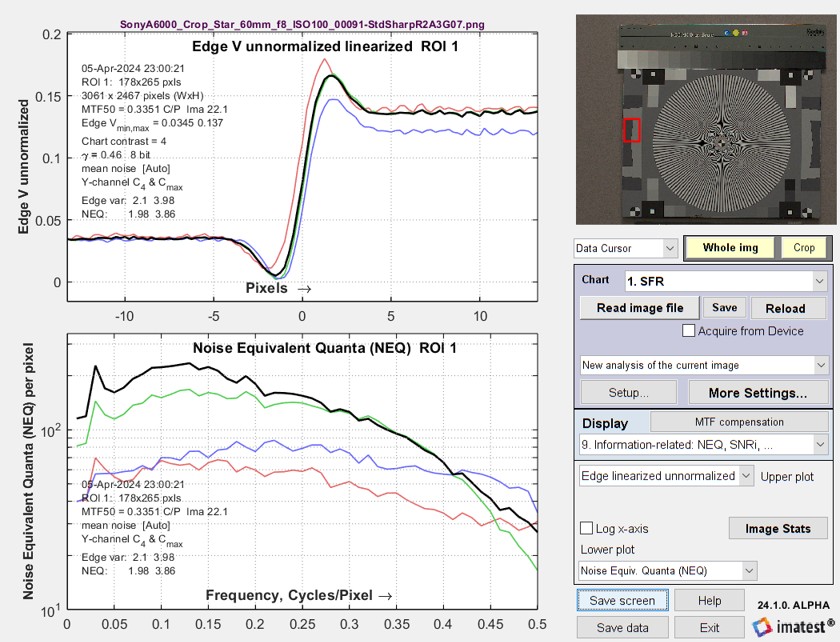
No image processing.Sony A6000. Straight out of LibRaw, unsharpened, NEQ is in the bottom plot. |
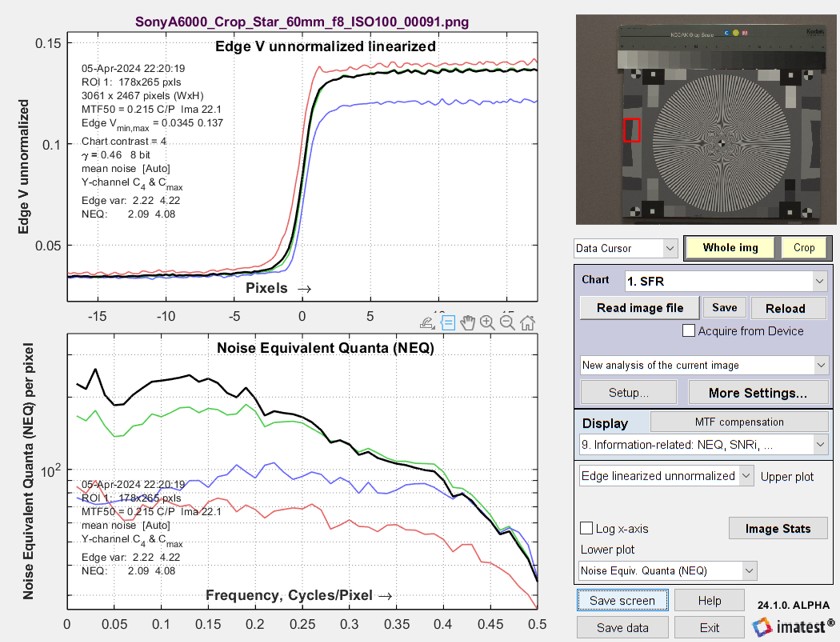 |
USM R2A3 Gaussian 0.7.The Sony A6000 image (above) has been filtered with a σ = 0.7 Gaussian Lowpass filter and an R2A3 USM sharpening, obtained with the Imatest Image Processing module.
NEQ(f) is very different from the unsharpened image: it is strongly boosted between 0.3 and 0.5 C/P. But we expected it to be nearly identical (for linear image processing). This discrepancy caused us a lot of grief in early 2024. Because we finally started to suspect that the MATLAB Unsharp Mask (USM) implementation (the imsharpen function) caused the problem, we developed a standard linear sharpening algorithm (a 2D version of the 1D sharpening described in the Sharpening page). We knew it was linear because we wrote the code. |
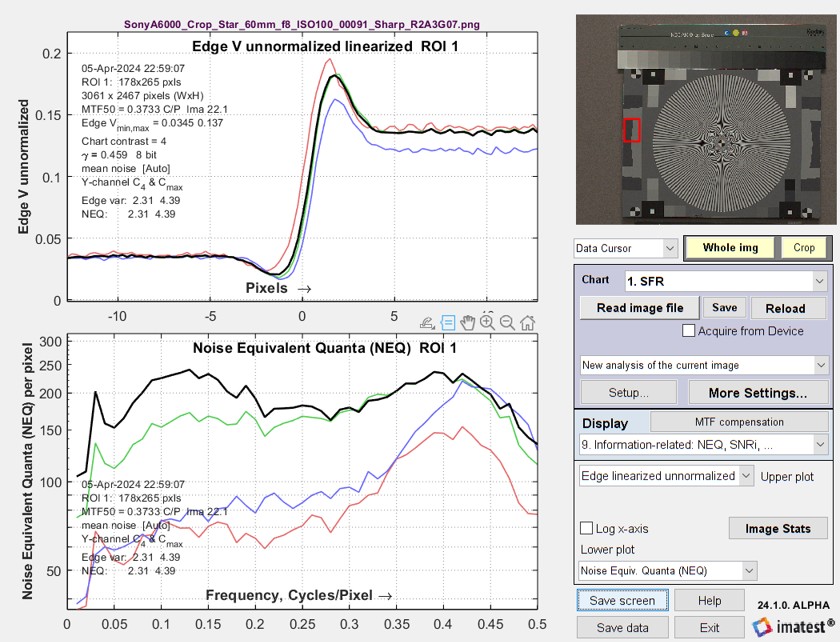 |
Standard sharpening
|
 |
|
The cause of the NEQ inconsistency was the nonlinearity of MATLAB’s USM processing, This is why we recommend Standard sharpening (which should be used with the Linearize function), |