Information capacity measurements from Slanted edges: Instructions

News: Imatest 23.1 (March 2023) (available in the Imatest Pilot program). New methods for calculating camera information capacity, Noise Power Spectrum (NPS), Noise Equivalent Quanta (NEQ), and Ideal observer SNR (SNRi) from slanted-edge patterns are now available.

The basic premise of this work is that Information capacity is a superior Key Performance Indicator (KPI) of imaging systems — better than sharpness or noise, which it incorporates. The revised 2020 white paper, “Camera information capacity from Siemens Stars“, briefly introduces information theory, describes the Siemens star camera information capacity measurement, then shows results (including the effects of artifacts).  A more recent white paper (2023), “Measuring Information Capacity with Imatest“, describes a method of measuring information capacity and related measurements (NPS, NEQ, SNRi, and more) from widely-used slanted edges. The slanted-edge method is faster, more convenient, and better for measuring the total information capacity of an image. It is recommended for most applications, but The Siemens star method is better for observing the effects of image processing artifacts (demosaicing, data compression, etc.).

 
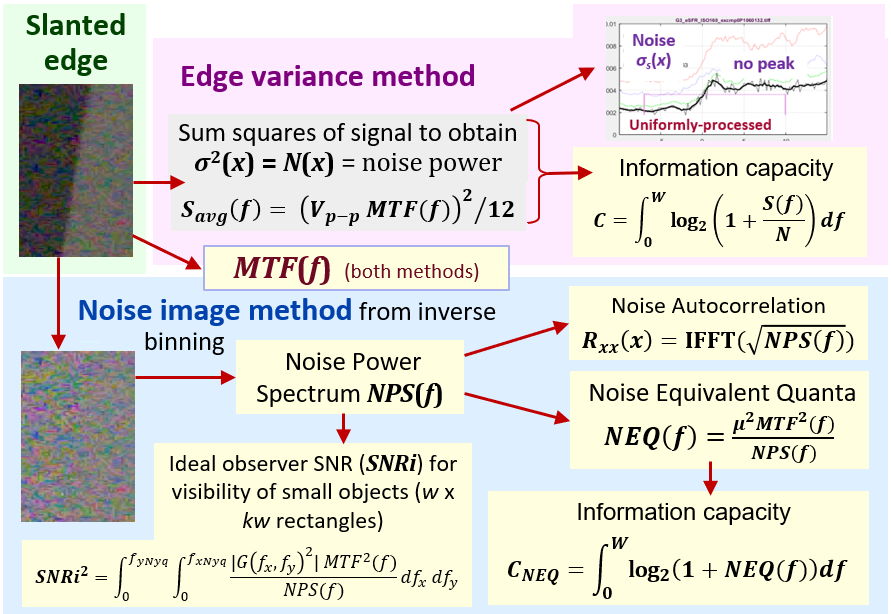
Introduction – Edge variance calculation – Noise image calculation – Diagram of the two methods  
Acquiring and framing – Running the MTF module – Signal averaging 
Key results – Edge/MTF plot – Edge/noise plot – 3D plot and Total information capacity – Noise image results –
Noise Power Spectrum (NPS) – Noise Equivalent Quanta (NEQ) – SNRi – C_SNRi – Noise Autocorrelation – 
Original & Noise image – Object visibility – Summary – Links 

Calculation summary page:  Introduction –  Edge variance calculation –  Noise image calculation 
Meaning of Information capacity  

Introduction to the new measurements

This page contains instructions for obtaining image quality measurements introduced in Imatest 23.1, released in March 2023. These measurements take advantage of newly-discovered properties of slanted edges– Imatest’s most widely used patterns for measuring MTF. Most are unfamiliar because they have been siloed in the medical imaging community, and have been traditionally difficult to perform. We describe two new measurement methodologies.

1. The Edge variance method, conveniently calculates camera information capacity.
2. The Noise image method uses a different approach to calculate information capacity and several additional image quality factors.

This page introduces the new calculations, shows how to obtain them, then presents Key Results.

Detailed algorithms are presented in Information capacity measurements from Slanted edges: Equations and Algorithms.
.

A: Edge variance calculation summary      Full details here 

Sum the squares of the scan lines to obtain the edge variance. 

The calculation is described in detail in the white paper, Measuring Camera Information Capacity with Imatest, and in the paper presented at Electronic Imaging 2023, “Measuring Camera Information Capacity with Slanted Edges“. The descriptions on this page are very concise; there is more detail in the two linked documents.

Starting with images of slanted edges, (Original ROI, below), typically made from a 4:1 contrast chart (chart contrasts between 2:1 and 10:1 are acceptable), the standard slanted-edge algorithm

1. finds the center of each scan line (taken in a direction approximately normal to the edge),
2. fits the centers to a polynomial curve, then,
3. depending on the location of the polynomial at the scan line, it adds the contents of the scan line to one of four bins.
4. These mean values of each bin are then interleaved to form a 4× oversampled edge, which has lower noise than any of the individual scan lines.

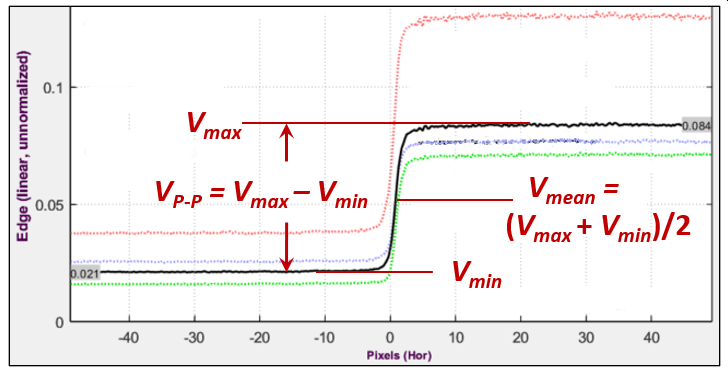
The Edge variance method adds another summation. The squares of each scan line are added to the appropriate bin to calculate the variance of the edge signal, σ², which is equivalent to its noise power, N. The mean signal amplitude for a uniformly-distributed signal of peak-to-peak amplitude V_P-P is \(S(f) = V_{P-P} MTF(f) / \sqrt{12}\) — a reasonable number to use for the information capacity calculation using the Shannon-Hartley equation, shown above.

The key results are,

C₄ is the Shannon capacity measured directly from (usually) 4:1 contrast ratio slanted-edges. It is calculated from the Shannon Hartley equation, using several assumptions (that the signal is uniformly distributed over the peak-to-peak signal measurement and the noise power spectral density (NPD) is flat). C₄ is a special case of C_n, for a n:1 contrast ratio (with ISO standard 4:1 strongly recommended) C_n is sensitive to chart contrast ratio and exposure, making it interesting for measuring performance as a function of exposure but not robust for calculating a camera’s maximum information capacity.

C_max is a much more stable measurement of the maximum information capacity for the camera starting with C₄ (for the 4:1 contrast chart). It is also insensitive to exposure, at least for linear sensors, where noise is a known function of signal voltage. 

B. Noise image calculation summary      Full details here 

Subtract a low-noise unbinned / reverse-projected ROI image to obtain a noise image.

This method involves inverting the ISO 12233 binning procedure. Noting that the 4× oversampled edge was created by interleaving the contents of 4 bins, we apply an inverse of the binning algorithm to set the contents of each scan line to its corresponding bin (Inverse binned… ROI, below). Since the inverse-binned image is nearly noiseless, a noise image can be created by subtracting the inverse-binned image from the original image. This image, adjusted to make the mean (zero) value middle gray, is illustrated as the Noise image ROI, below. 

Key measurements from the Noise image method. Many are used in medical radiology.

Measurement	Description
Noise Power Spectrum, NPS(f)	NPS was implicitly assumed to be constant (white noise) in the Edge variance method.
Noise Equivalent Quanta, NEQ(f) and NEQinfo(f)	measures of frequency-dependent signal-to-noise ratio (SNR). \(NEQ(f) = \mu^2\ MTF^2(f) / NPS(f)\text{,  where }\mu = V_{mean}\) has been used for quantifying medical image quality, but are much less familiar in general imaging. NEQ(f) is equivalent to the number of quanta detected by the sensor when photon shot noise is dominant. It is appropriate for calculating Digital Quantum Efficiency (DQE), when the density of quanta reaching the image sensor is known. NEQinfo(f) is derived from \(\mu = V_{P-P} / \sqrt{12}\), making it well-suited for calculating information capacity CNEQ.
Information capacities C4-NEQ and Cmax-NEQ	correspond to C4 and Cmax from the Edge variance method, but are derived from NEQinfo(f). They are close, but not identical.
Ideal observer Signal-to-Noise Ratio, SNRi	From Skorka and Kane [9], “The Ideal Observer is a Bayesian decision maker that maximizes the statistical precision of a hypothesis test with two possible outcomes.” SNRi as we present is, is a metric of the detectability of small objects (squares or rectangles), typically of low contrast.
Noise autocorrelation	The inverse Fourier transform of the Noise Voltage Spectrum. Related to sensor electrical crosstalk.

 

Why two methods? The Edge variance was developed first, in late October 2022. It was presented at the Electronic Imaging 2022 conference. The Noise image method was developed in February 2023, about a month after the conference. It measures more image quality parameters than the Edge variance method.  We currently recommend the Noise image method because we believe the camera information capacity measurement is slightly more accurate. The reason: it calculates the Noise Power Spectrum, while the Edge variance assumes the NPS is flat (white). On the other hand, The Edge variance method can provide useful (if imperfect) results for bilateral-filtered images (most JPEGs from consumer cameras), while the Noise image method is only recommended for uniformly or minimally-processed images.

Summary of the two methods

Acquire the image

 

Acquire a well-exposed image of any slanted-edge test chart (SFRplus, eSFR ISO, Checkerboard, SFRreg, or SFR) in even, glare-free light. Chart edge contrast ratio should be 4:1 (the ISO 12233 standard) where possible. The limits are 2:1 to 10:1. For the most part, acquiring the image is identical to standard MTF measurements.

Exposure consistency is important because exposure affects the information capacity measurement. (Exposure has only a second-order effect on MTF measurements.) The mean pixel level of a perfectly exposed slanted-edge region should be in the range of 0.20 to 0.26, but there is plenty of latitude as long is the image isn’t saturating. 

For best results the slanted edge should be 100 pixels or more along the edge. Fewer pixels will work, but the results will be less consistent. 

 

Run the MTF calculation module

Run either an appropriate Rescharts module (interactive; recommended for starting and making settings — SFRplus Setup, eSFR ISO Setup, SFRreg Setup, or Checkerboard Setup in the second column in the Imatest main window or an appropriate fixed, batch-capable module (SFR, SFRplus Auto, eSFR ISO Auto, SFRreg Auto, or Checkerboard Auto buttons in the left column).

Edge/MTF display — In the Settings window, select the appropriate setting in the Information capacity display dropdown menu. It may be somewhat inconspicuous. Calculating information capacity slows down operations slightly. Two examples are shown below. 

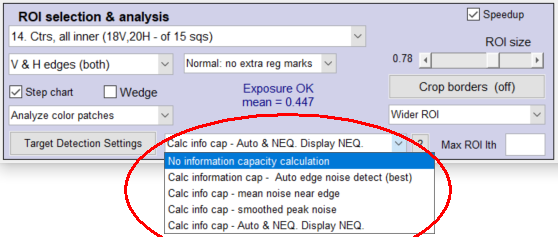information capacity noise calculation setting, from a crop of the Rescharts Settings window

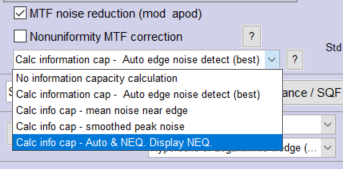Information capacity noise calculation setting, from left side of More settings window

The full windows and complete instructions are in SFRplus, eSFR ISO, Checkerboard, SFRreg, or SFR.

The reason for the different Edge variance noise calculations is 

• uniformly or minimally-processed images, often converted in the computer from raw images, pictured here, have relatively uniform noise, which is somewhat signal-dependent. There is no noise peak near the transition. Hence the mean edge noise in the ROI is most appropriate.
• bilateral-filtered images, including most JPEGs from consumer cameras, pictured here, are sharpened near the transition and noise-reduced (lowpass-filtered) elsewhere. Hence the average noise would be too low to represent system performance. Hence the (smoothed) peak noise is most appropriate.
• The presence or absence of a peak can be used to detect bilateral filtering (for setting 2: Auto edge noise detection), but it’s not entirely accurate  since soft images may exhibit little peak. 

If an information capacity calculation is selected (2-5, below), both Edge variance and Noise image calculations are performed. These settings affect the Edge/MTF display, which has limited space. Results from both methods are displayed in the Noise Spectrum, NEQ, SNRi plot when Results summary is selected for the lower plot.

#	Setting	Description	Best for
1.	No information capacity calculation	slightly faster than calculating information capacity. About the only time it’s appropriate is for high-speed realtime image acquisition.	Fastest, but not by much since info cap calculations are turned off during reloads.
2.	Calculate info cap:  Auto edge noise detection	Selects the noise calculation method depending on the detection (presence or absence) of a noise peak. Often recommended, but we have found that it sometimes misses the peak in bilateral-filtered images. One of the next two choices is recommended if you predominantly use one file type (either minimally/uniformly processed or bilateral-filtered).	for unknown image processing: “black box”
3.	Calculate info cap using mean edge noise (default) (Method (1))	for images converted from raw with minimal or uniform processing (no bilateral filtering).	for uniformly / minimally-processed images
4.	Calculate info cap using smoothed peak noise (Method (2))	for bilateral-filtered images, which includes most JPEG images from consumer cameras. It works for uniformly-processed images, but gives less stable results than Method (1).	for bilateral-filtered images (most consumer camera JPEGs)
5.	Calculate info cap – Auto & NEQ  Display NEQ	Display the results of the Noise image method in the Edge/MTF plot. Display the results of both methods, with Auto edge noise detection for the Edge variance plots, in the Edge/MTF display. This is our current recommendation for minimally/uniformly processed images.	Best all around

 

When OK is pressed the image is analyzed. Any of several displays can be selected in Rescharts, but only a few (shown below) are related to information capacity. The same results can be obtained from running fixed modules. 

From the Rescharts interactive interface, the noise calculation can always be set (or changed) from a dropdown menu on the left of the More settings window.  This setting is also in the SFR and Rescharts SFR Settings windows.

 

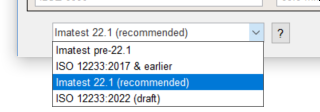
In the lower-left of the More settings window, choose one of the Imatest  edge calculations, preferably Imatest 22.1 (recommended). At this writing it produces the most reliable results. 

Tips & recommendations

Uniformity — The chart should be illuminated as uniformly as possible. Simple (first-order) nonuniformity can be corrected, but charts that are not mounted flat may have nonuniformities (kinks) that cannot be corrected, resulting in serious degradation of information capacity.

 JPEG artifacts — with low-quality JPEGs can be really ugly and seriously degrade measurements. The example on the right, enlarged 4×, illustrates both JPEG artifacts and kinks. This image had significant noise reduction at a distance from the edge, and low quality compression may have been applied in the website used to transmit the image. If an image needs to be saved as a JPEG to keep it small enough for an email attachment, make the JPEG very high quality.

Smoothing rough results with signal averaging

Sometimes results such as MTF or NEQ (or any results) can be rough for noisy images. This happens because slanted-edge Regions of Interest (ROIs) are often smaller than optimum. A  reliable fix for this issue is signal averaging: acquiring multiple identical images, then averaging them for analysis. Averaging N_avg signals improves the Signal-to-Noise Ratio (SNR) by the square root of N_avg (an improvement of 3 dB for every doubling of N_avg).

For information capacity/SNRi/NEQ calculations, Noise power is multiplied by the number of averages, N_avg. This does not cause a systematic change in the results — it just makes them more consistent.

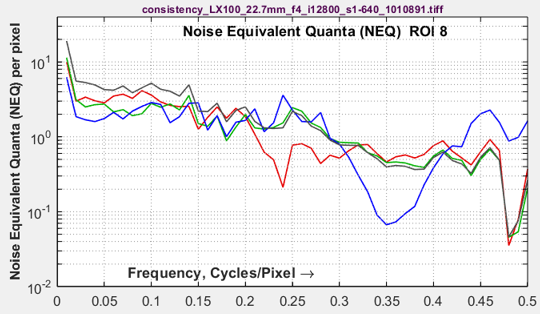
Here are examples of the improvements from signal averaging.

Noisy image (ISO 12800)	Noisy image, navg = 10 averages

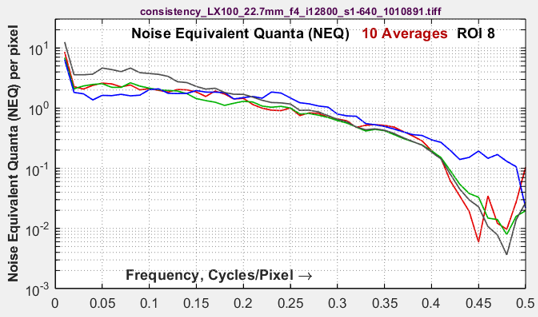Benefits of signal averaging

Signal averaging works with almost any Imatest analysis module. It is particularly valuable for Random/Spilled Coins and Log F-Contrast.

Instructions for signal averaging

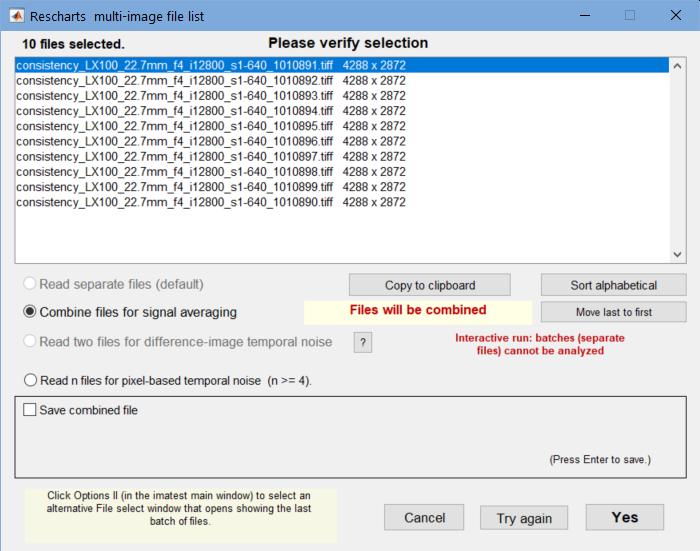
• Read a batch of N images (using the usual methods of selecting multiple files). The settings window shown below appears. A warning will appear if the files are not equal in size.

• Select Combine files for signal averaging. The Save combined file checkbox is optional.
• if settings are correct, press Yes. The analysis will proceed.

Key results

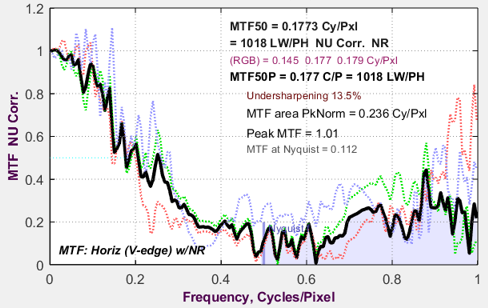
Edge/MTF plot

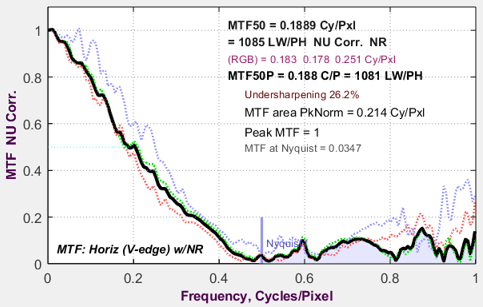
Information capacity (for the individual edge) has been added to the upper (Edge) plot. Nothing else has changed.

The image below is from a raw-converted eSFR ISO chart image from a high quality compact camera.

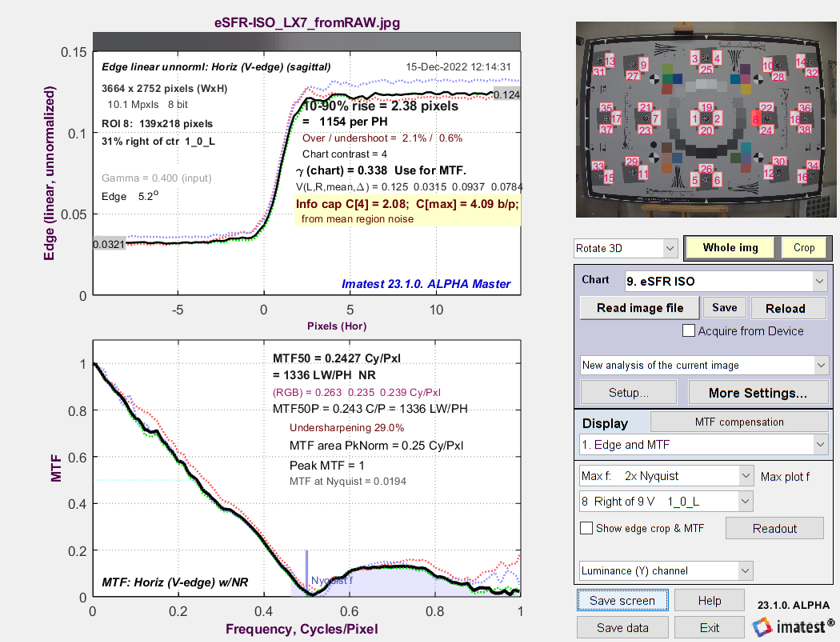Edge/MTF Results from eSFR ISO image converted from raw with minimal processing

Both information capacity C₄ (for 4:1 contrast charts; very sensitive to exposure) and C_max (maximum information capacity; relatively insensitive to exposure) are displayed. 

Edge & Info Capacity Noise

This is a variant of the Edge and MTF plot. The top plot is similar (though the Line Spread Function — the derivative of the edge — is of special interest for this plot).

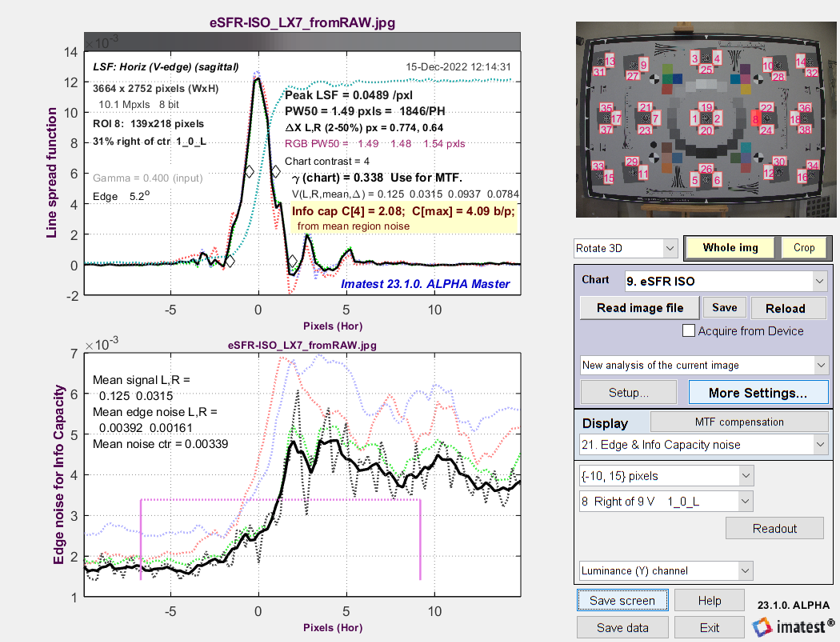Line Spread Function (LSF) and signal-dependent noise σ from
eSFR ISO image converted from raw with minimal processing

The solid line is the noise smoothed by a rectangular kernel with width = 5 (4× oversampled) pixels (1.25 original pixels). Note that the noise is very rough and that there is no distinct peak near the edge transition. From observing regions of the chart, the bumps on the noise curve appear to be random and not repeatable.

Now it gets interesting. The image used for the above plots is derived from a raw image with minimal processing (straight gamma curve; no sharpening or noise reduction — and definitely NO bilateral filtering). Here are results for the in-camera JPEG from the same acquisition. Note the large noise peak near the edge. We use Method (1) to calculate noise for the Shannon-Hartley equation, which takes the average over a fairly wide region near the edge.

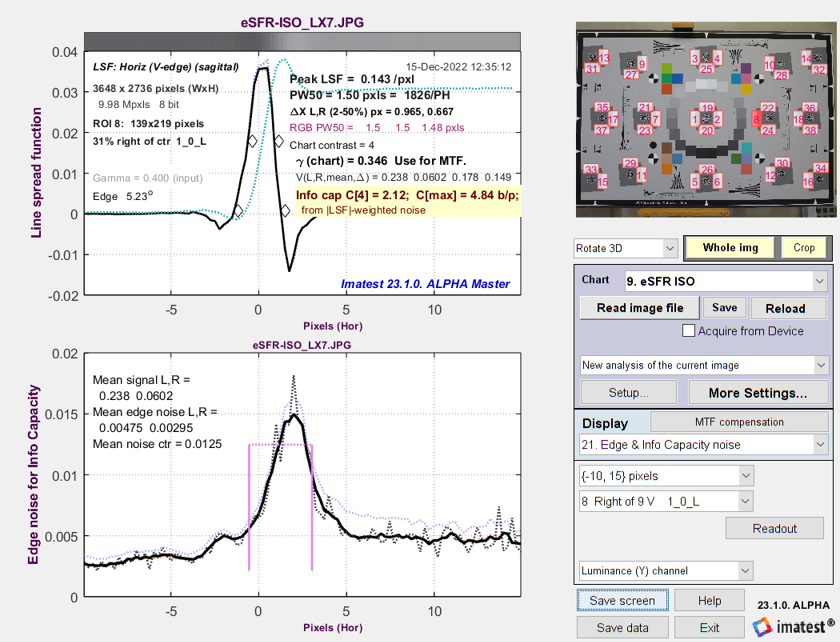Line Spread Function (LSF) and signal-dependent noise σ from
eSFR ISO image captured as a JPEG (with strong sharpening and bilateral filtering)

Method (2): Calculate noise for info cap using the maximum value of the smoothed edge noise. This method is recommended for bilateral-filtered JPEGs because it uses a relatively narrow region near the noise peak for measuring noise. Information capacity C₄ = 3.11 b/p is only slightly higher than for the TIFF: 3.0 b/p. If Method (1) (averaging over a large area, which doesn’t emphasize the peak) is chosen, C₄ = 3.84 b/p: significantly larger than the raw measurement, and clearly not accurate.

3D plot and total information capacity

C₄ and C_max have been added to the available 3D plots.

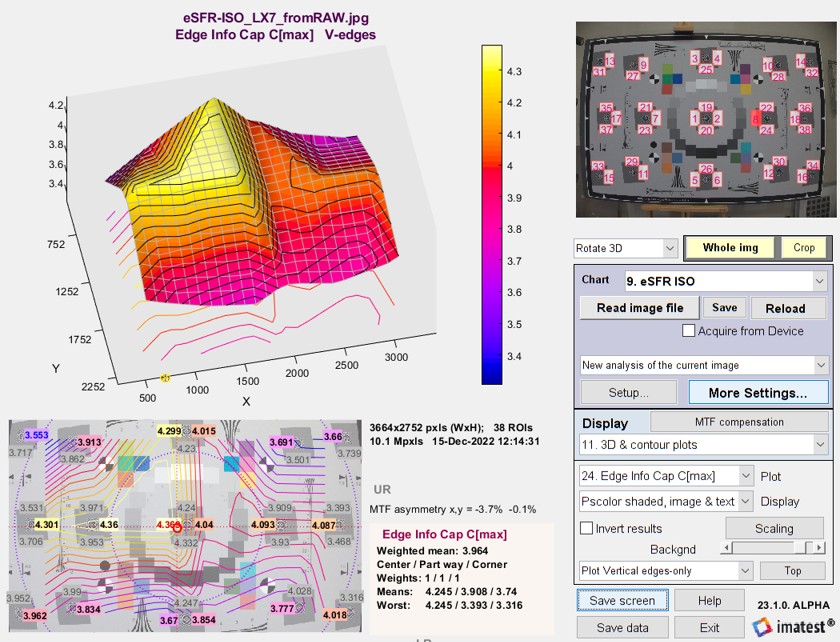3D plot of Edge Information capacity C₄

The total information capacity C_total (referenced to the signal level: in this case 4:1) is calculated by multiplying the weighted mean (with all weights are set to 1 for the two information capacity plots) in bits per pixel by the total number of megapixels. It is displayed next to the mean information capacity (in bits per pixel).

In the above image, C_total = 2.847 bits/pixel × 16 megapixels = 45.44 megabits. The display shows  Edge Info Cap C_max  Mean: 2.847;  total Mb: 45.44.

Results for Noise image calculation: NPS, NEQ, and SNRi

The new results (NPS, NEQ, SNRi) and an old one (MTF) can be displayed in the 9. Noise Spectrum, NEQ, SNRi plot. This plot shows results for all available color channels. A 24 megapixel Micro Four-Thirds camera with a high quality 60mm lens set to f/8 and ISO 100 was used to obtain these results.

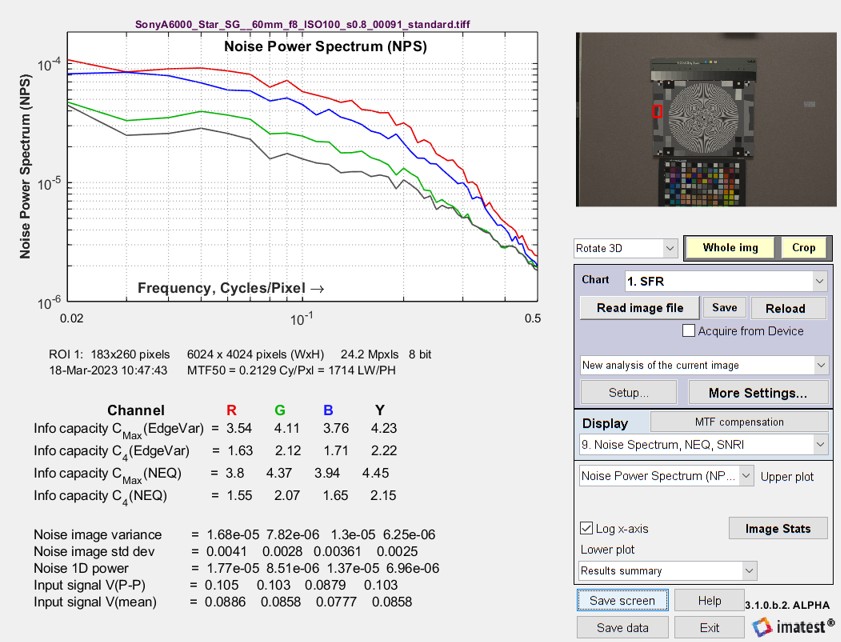Noise Power Spectrum (NPS) plot and results summary from Rescharts

There are several independent choices for the upper and lower plots in two dropdown menus, located just below the  Display  area on the right of the figure.

Upper or Lower plot	Display settings	Lower plot-only
Noise Voltage Spectrum Noise Power Spectrum (NPS)      (shown above) Noise Equivalent Quanta (NEQ) MTF* Edge linearized unnormalized* Noise autocorrelation SNRi 2D square w x w SNRi 2D rectangle w x 4w C_SNRi square w x w experimental  *for checking inputs to NEQ calculation (These plots are available elsewhere.)		Original image crop Unbinned image crop       (Reverse-projected; low noise) Noise image crop  (Original – Noise) Results summary  (Shown above) SNRi 2D square w x w SNRi 2D rectangle w x 4w Square visibility image Square visibility – LARGE Noise Voltage Spectrum Noise Power Spectrum (NPS) Noise Equivalent Quanta (NEQ) MTF* Edge linearized unnormalized* Noise autocorrelation C_SNRi square w x w experimental

 

The checkbox between the two dropdown menus (set to Log x-axis above) lets you select a linear or logarithmic x-axis in the upper plot.

Upper or lower plots  displayed on the left of the Rescharts window (upper or lower)

For plots with frequency in the x-axis, the Frequency display can be set to linear or logarithmic (Log x-axis is checked in the Display area, above). 

These plots can be displayed for convenient comparison — valuable for exploring the relationships between results — in either the upper or lower positions. It is possible, though not recommended, to display the same result in the top and bottom.

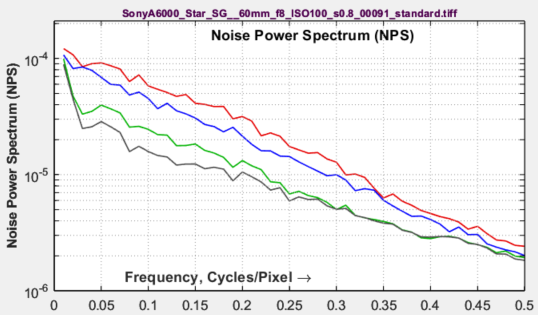
Noise Voltage or Power Spectrum (NPS) The NPS (upper) plot is shown above with a logarithmic x-axis and on the right with a linear x-axis (selected by a checkbox). The Noise Power and Voltage Spectrum plots have the same shape: only the y-axis labels are different. The 1D Noise Power or Voltage spectrum is derived from a 2D Fourier transform (FFT) of the noise image. The initial 2D FFT has zero frequency at the image center. The image is divided into several annular regions, and the average noise power is found for each region. NPS is primarily used to check the input to the NEQ plot.   Equations/algorithms
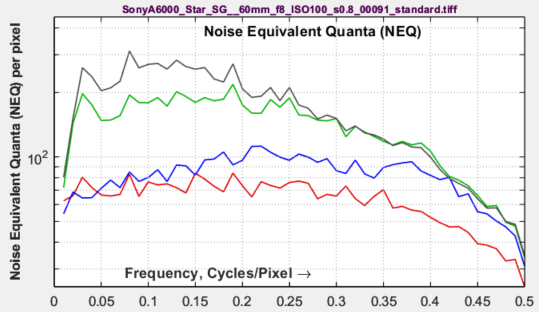
Noise Equivalent Quanta (NEQ) The standard NEQ used in the plot is based on the mean signal voltage, Vmean, shown above. A different voltage, VP-P /sqrt(12), is used to calculate NEQ-based information capacity, CNEQ.  The NEQ plot is rough because of the relatively small size of the slanted-edge ROIs (Regions of interest).   Equations/algorithms
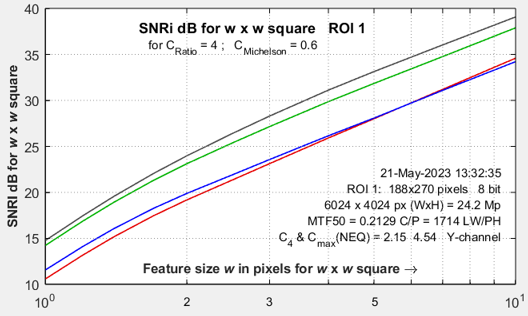
Ideal observer Signal-to-Noise Ratio (SNRi) SNRi is an indicator of the detectability of small objects. It can be displayed for three feature types: a square of sides w and rectangles of sizes w × 2w and w × 4w for w = the smaller side in pixels.  SNRi is a new addition to Imatest. We’ll have more to say about it when we gain experience in using and interpreting it. It is discussed in detail in papers by Paul Kane [8] and Orit Skorka and Paul Kane [9].   Equations/algorithms
SNRi information capacity: CSNRi  (new and experimental) CSNRi is a new (May 2023) experimental measurement that takes advantage of the fact that the argument of the SNRi2 integral has units of Signal-to-Noise Ratio power, and hence can be used in the Shannon-Hartley equation, CSNRi is not yet fully validated, but it’s promising (we are working on it). Plots are generally more readable and easier to interpret than SNRi. For images with poor MTF, CSNRi increases more slowly for small widths w. The (rough) asymptotic value is close (though not identical) to C4(NEQ). CSNRi . should be available in the pilot program by June 2023. (I’m not sure of the release schedule).  Equations/algorithms
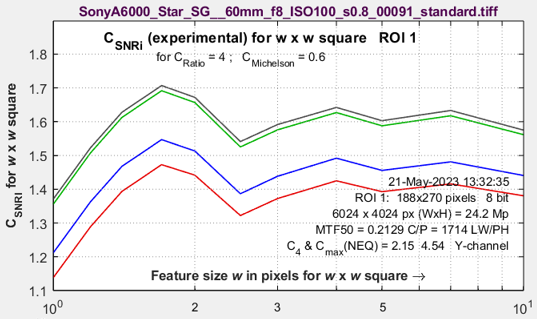Modulation Transfer Function (MTF) Available here for convenience because MTF is used in the NEQ calculation. It looks a little different from MTF in the standard Edge/MTF plot because the y-axis is logarithmic.
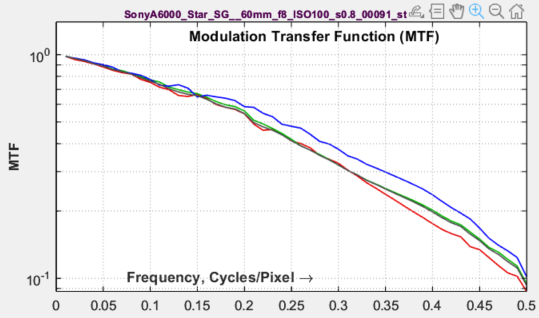Edge voltage unnormalized  Displayed primarily to check input for the NEQ calculation. It’s often interesting to compare peak-to-peak amplitudes of the different channels.
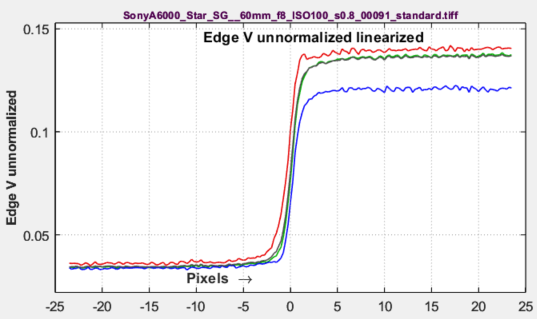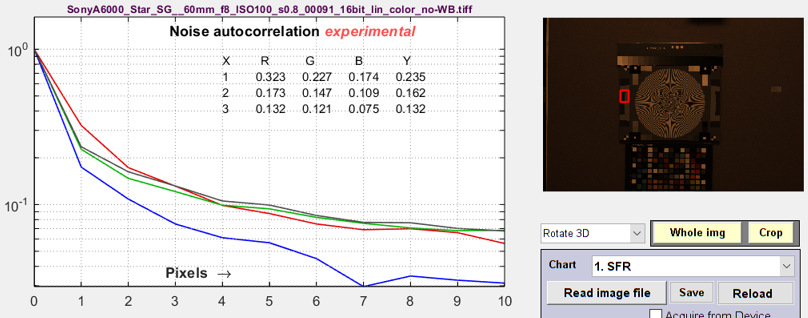
Noise autocorrelation (related to sensor electrical crosstalk) This plot has been included more for R&D than for regular testing to examine the hypothesis that the noise power spectrum (and autocorrelation) indicate the amount of electrical crosstalk of image sensor when the effects of demosaicing and fixed-pattern noise are removed and the primary noise source is photon shot noise. The idea behind the hypothesis is that light incident on the sensor is entirely uncorrelated, so that if there were no crosstalk the noise would be white.  This image on the right was white-balanced. The noise autocorrelation curve is the inverse Fourier transform of the noise spectrum, based on the author’s limited understanding of the Wiener-Khinchin theorem.
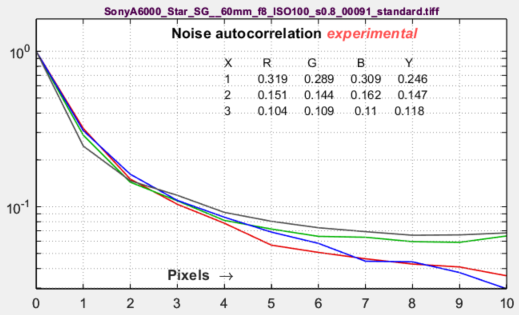The image on the right was not White-Balanced. The red channel has a larger autocorrelation distance than the other channels, as we would expect.  Click on the image to enlarge it. A similar autocorrelation plot can also be obtained from a flat field image in the Image Statics module. Illumination nonuniformity was corrected to decrease the autocorrelation at large distances.   Equations/algorithms

 

Lower plots  Displayed in the lower-left of the Rescharts window

Image ROI crops (original, unbinned, noise) We illustrate crops of the ROI here for a noisy image (ISO 12800), where the difference between the original and unbinned image is easy to see.  The images are all gamma-encoded for display. The noise image on the right has been lightened (its actual mean is zero) and contrast-boosted. The effectiveness of the de-binning for removing noise is impressive. It is the basis for the Noise image calculations (NEQ, SNRi, etc.).   Equations/algorithms	original unbinned noise
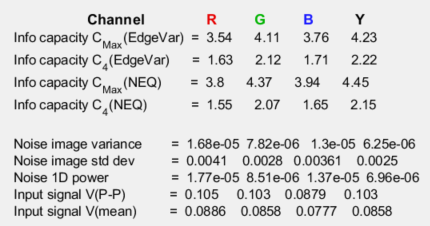
Results summary The first two lines contain a summary of image properties. The bottom group of lines contain several variables used in program development to check the accuracy of the calculations. The primary results are the Information capacities in the middle. C4(EdgeVar) and Cmax(EdgeVar) are derived from the Edge Variance method. C4(NEQ) and Cmax(NEQ) are derived from the the Noise image method (designated NEQ because they’re calculated directly from NEQ). They are not identical because the Noise image method uses the measured Noise Power Spectrum, while the Edge Variance method assumes white noise power.
Object visibility The LARGE option covers both the upper and lower plot areas for improved visibility. Predicting object visibility for small, low contrast squares or 4:1 rectangles is the goal of SNRi measurements. The SNRi prediction begs for visual confirmation.  We have developed a display for Imatest that does this with the contents of a real slanted-edge image and a bit of trickery. This display is different from most other Imatest displays in that it is intended for perceptual judgment, based on the original image (it’s hard to make perceptual judgments on slanted edges) and the calculated Line Spread Function (transformed into 2D).   The results on the right are for a noisy image from a Micro Four-Thirds camera at ISO 12800. The sides of the squares are w = 1, 2, 3, 4, 7, 10, 14, and 20 pixels. The original chart had 4:1 contrast ratio (light/dark = 4), equivalent to a Michelson contrast CMich ((light-dark)/(light+dark)) of 0.6. The outer squares have CMich = 0.6, while the middle and inner squares have CMich = 0.3 and 0.15, respectively. How to use these images — Inconspicuous magenta bars near the margins are designed to help finding the small squares, which can be hard to see. The SNRi curves are (initially, at least) for the chart contrast — with 4:1 (the ISO 12233 standard) strongly recommended. The outer patches correspond to the SNRi curves, and according to the Rose theory, SNRi of 5 (14 dB) should correspond to the threshold of visibility. These can be compared with the SNRi curve.   Equations/algorithms

Summary

• Shannon information capacity C has long been used as a measure of the goodness of electronic communication channels. It specifies the maximum rate at which data can be transmitted without error if an appropriate code is used (it took nearly a half-century to find codes that approached the Shannon capacity). Coding is not an issue with imaging. Rodney Shaw’s paper from 1962 [10] is a particularly good example of measuring C for photographic film— it wasn’t easy back then. 
• C is ordinarily measured in bits per pixel. The total capacity is \( C_{total} = C \times \text{number of pixels}\).
• The channel must be linearized before C is calculated, i.e., an appropriate gamma correction (signal = pixel level gamma, where gamma ≅ 2.2 for images in standard color spaces such as sRGB or Adobe RGB) must be applied to obtain correct values of S and N. The value of gamma (close to 2) can be determined from runs of any of the Imatest modules that analyze grayscale step charts: Stepchart, Colorcheck., Color/Tone, Multitest, SFRplus, or eSFR ISO. But in most cases it can be determined from the edge image if the chart contrast is entered and Use for MTF is checked.
• We hypothesize that C can be used as a figure of merit for evaluating camera quality, especially for machine vision and Artificial Intelligence cameras. (It doesn’t directly translate to consumer camera appearance because they have to be carefully tuned to reach their potential, i.e., to make pleasing images). It provides a fair basis for comparing cameras, especially when used with images converted from raw with minimal processing.
• Imatest calculates the Shannon capacity C for the Y (luminance; 0.212*R + 0.716*G + 0.072*B) channel of digital images, which approximates the eye’s sensitivity. It also calculates C for the individual R, G, and B channels as well as the C_b and C_r chroma channels (from YC_bC_r).
• Shannon capacity has not been used to characterize photographic images because it was difficult to calculate and interpret. But now it can be calculated easily, its relationship to photographic image quality is open for study.
• Since C is a new measurement, we are interested in working with companies or academic institutions who can verify its suitability for Artificial Intelligence systems.

Note: A slanted-edge information capacity measurement used prior to Imatest 2020, used primarily to obtain total information capacity from Siemens star measurements, has been deprecated completely because it was not sufficiently accurate.

 

Links  (more links in the White Paper)

1. C. E. Shannon, “A mathematical theory of communication,” Bell Syst. Tech. J., vol. 27, pp. 379–423, July 1948; vol. 27, pp.
   623–656, Oct. 1948.
2. C. E. Shannon, “Communication in the Presence of Noise”, Proceedings of the I.R.E., January 1949, pp. 10-21.
3. Wikipedia – Shannon Hartley theorem  has a frequency dependent integral form of Shannon’s equation that is applied to both Imatest’s sine pattern and slanted edge Shannon information capacity calculation. 
4. I.A. Cunningham and R. Shaw, “Signal-to-noise optimization of medical imaging systems”, Vol. 16, No. 3/March 1999/pp 621-632/J. Opt. Soc. Am. A 
5. Brian W. Keelan, “Imaging Applications of Noise Equivalent Quanta”  in Proc. IS&T Int’l. Symp. on Electronic Imaging: Image Quality and System Performance XIII,  2016,  https://doi.org/10.2352/ISSN.2470-1173.2016.13.IQSP-213.
6. Michail C, Karpetas G, Kalyvas N, Valais I, Kandarakis I, Agavanakis K, Panayiotakis G, Fountos G., Information Capacity of Positron Emission Tomography Scanners. Crystals. 2018; 8(12):459. https://doi.org/10.3390/cryst8120459. 
7. Christos M. Michail, Nektarios E. Kalyvas, Ioannis G. Valais, Ioannis P. Fudos, George P. Fountos, Nikos Dimitropoulos, Grigorios Koulouras, Dionisis Kandris, Maria Samarakou, Ioannis S. Kandarakis, “Figure of Image Quality and Information Capacity in Digital Mammography”, BioMed Research International, vol. 2014, Article ID 634856, 11 pages, 2014. https://doi.org/10.1155/2014/634856. 
8. Paul J. Kane, “Signal detection theory and automotive ima­ging”, Proc. IS&T Int’l. Symp. on Electronic Imaging: Autonomous Vehicles and Machines Conference,  2019,  pp 27-1 – 27-8,  https://doi.org/10.2352/ISSN.2470-1173.2019.15.AVM-027.
9. Orit Skorka, Paul J. Kane, “Object Detection Using an Ideal Observer Model”,  IS&T Int’l. Symp. on Electronic Imaging: Autonomous Vehicles and Machines,  2020,  pp 41-1 – 41-7, https://doi.org/10.2352/ISSN.2470-1173.2020.16.AVM-041.
10. R. Shaw, “The Application of Fourier Techniques and Information Theory to the Assessment of Photographic Image Quality”, Photographic Science and Engineering, Vol. 6, No. 5, Sept.-Oct. 1962, pp.281-286. Reprinted in “Selected Readings in Image Evaluation,” edited by Rodney Shaw, SPSE (now SPIE), 1976. A fascinating and difficult calculation of information capacity of photographic film. Available for download
11. X. Tang, Y. Yang, S. Tang, Characterization of imaging performance in differential phase contrast CT compared with the conventional CT: Spectrum of noise equivalent quanta NEQ(k), Med Phys. 2012 Jul; 39(7): 4467–4482. Published online 2012 Jun 29. doi: 10.1118/1.4730287
    . 

The math and algorithms behind the calculations are presented in Information capacity measurements from Slanted edges: Equations and Algorithms.