This page describes Uniformity (formerly Light Falloff ) features available with Imatest Master, i.e., not available in Studio. Uniformity was originally intended to measure lens vignetting (the falloff in illumination at the edges of the image), but it has been enhanced to measure a variety of image nonuniformities— resulting from the lens, illumination, or sensor— including color shading, noise distribution, and spots from dust (though Blemish Detect is much better at handling visible spots). Basic instructions are found in Using Uniformity, Part 1.
| New in Imatest 5.0 Uniformity can test for ISO 18844 flare (veiling glare). New in Imatest 4.0 Pass/Fail results can be displayed immediately with the Pass/Fail monitor. New in Imatest 3.10 Most Uniformity features (except for Noise detail) are available in Blemish Detect. Clusters of hot/dead pixels can be detected. |
Input settings
The following settings are available in all Imatest versions:
-
- Title Defaults to the file name. You can change it if you wish.
- Display Uniformity contour plots (Plot area; on by default).
Turns the main light falloff contour plots off or on. Normally on (checked), but may be turned off by Imatest Master users interested in other results, such as hot/dead pixels and color shading. Four display options are available. Normalized refers to the first (level) plot only.
Examples on Using Uniformity, Part 1.
| Contours superposed on image (not normalized) |
| Contours superposed on image (normalized to 1) |
| Pseudocolor with colorbar (not normalized) |
| Pseudocolor with colorbar (normalized to 1) |
- Speedup When checked, several results (those that require significant calculation time) are not calculated (and hence not saved in the CSV output file) if the corresponding plot is not selected. This can save significant time in production environments. If you need to use Speedup, you should run Uniformity with and without Speedup checked and examine the CSV output file to see if it contains the results you require.
- Gamma The default value of gamma, 0.5, is typical for digital cameras. Gamma affects only the second figure (the light falloff measured in f-stops); it has no effect on the first figure. Gamma can be measured by Stepchart using any one of several widely-available step charts. (Reflection charts are easiest to use but transmission charts can also be used to measure dynamic range.) Some issues in calculating gamma are discussed below the second figure.
- Corner and side regions (default 32x32 pixels) allows you to select the areas at the corners and sides of the images to be analyzed. Choices include 10x10 pixels, 32x32 pixels, 1% (min. 10x10), 2% (min. 10x10), 5%, and 10%. These regions can be used as the reference for the Color shading ΔE and ΔC calculations.
- Crop pixels near borders (L, R, T, B) (Settings area). If checked, the image is cropped by the number of pixels indicated near the left, right, top, and bottom borders. Several cropping (ROI selection) options are available by clicking Settings, Options and Settings… in the Imatest main window. These incluce
Don’t ask to crop. (Use settings in LF input dialog box.) Select crop by dragging cursor. Ask to repeat crop for same sized image. Select crop by dragging cursor. Do not ask to repeat crop. Although the first option (Don’t ask to crop…) was the default prior to Imatest 2.3.12, the second option (Select crop by dragging cursor. Ask to repeat crop for same sized image), which is similar to the ROI selection in SFR, may be preferred.
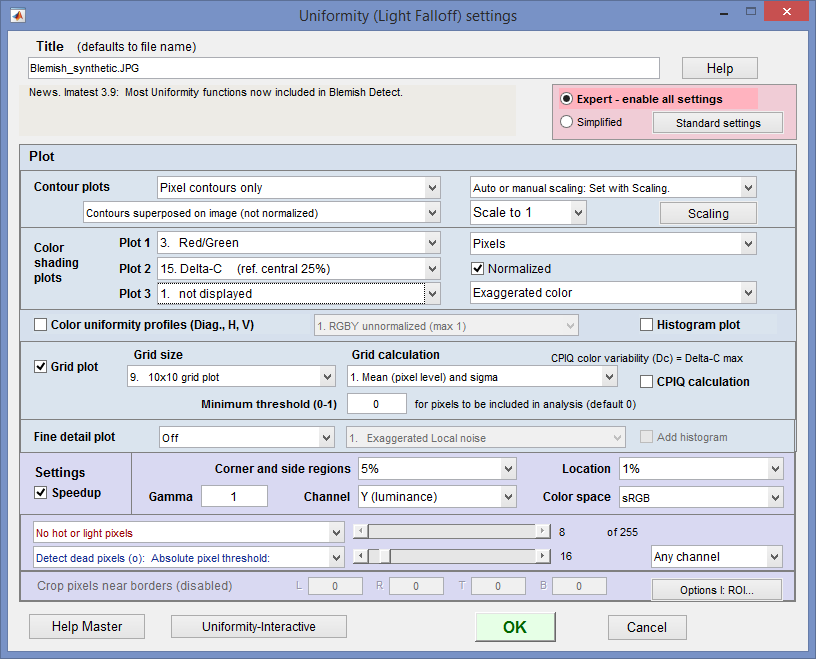
Uniformity settings window (for Imatest Master).
The following options are available in Imatest Master (not in Studio):
- Color shading (nonuniformity) Display the color nonuniformity, i.e., the quotient of or difference between two of the three (R, G, B) channels or one of the L*a*b* color difference metrics (ΔE = sqrt(ΔL*2 + Δa*2 + Δb*2 ), ΔC = sqrt(Δa*2 + Δb*2 ), ΔE94, ΔC94, ΔE00, ΔC00 ), referred to the center of the image (either the central region, with size specified in the Corner and side regions box or the central 25% by area). Color shading often results from the angle at which light strikes the sensor. It tends to be worst in sensors with tiny pixels. Several options are available. [Note: the center of the image is used for the reference for calculating ΔC and ΔE in the Color shading plots, but for the grid plot, which implements the CPIQ Phase 2 specification, the mean of the entire image is used as the reference for calculating ΔC and ΔE.]
- Color shading Select not displayed (turns off plot), Red/Blue, Red/Green, Green/Blue, or ΔE or ΔC (various flavors & reference regions). Red/Blue (the extremes of the spectrum) is the most popular choice for displaying shading. for (plot units). To the right of the Color shading box. Select Pixels (gamma-encoded), Intensity (linear), or f-stop difference. Grayed out if ΔE or ΔC metrics are selected.
Pixels Displays the ratio of the the pixel values for the selected channels. If Normalized is checked, the plot is normalized to 1.0 (maximum). Intensity (linear) Removes the gamma encoding of the image file using the value of Gamma entered and displays the ratio of the intensities for the selected channels. If Normalized is checked, the plot is normalized to 1.0 (maximum). F-stop Displays the f-stop difference between the selected channels. If Normalized is checked, the plot is normalized to 0 (maximum). - Display Select the display type. Four choices.
Examples are shown belowExaggerated color 2D. Increases the color saturation to increase the visibility of color nonuniformities. Pseudocolor 2D 3D Pseudocolor, shaded, auto-scaled. Shading emphasizes contour shapes. 3D Pseudocolor, auto-scaled. - Normalized (Checkbox) If checked (the default), the shading plot is normalized to a maximum of 1 for quotient displays (Red/Green, etc.) Affects only the plot, not the numeric values beneath the plot. The unnormalized maximum and minimum and other values are displayed beneath the plot.
- Extra smoothing This increases the smoothing of the contour and shading plots. Checked by default and strongly recommended. When unchecked the contour and color shading plots are much bumpier, more susceptible to noise, and slower. This checkbox may be removed in a future version.
- Color shading Select not displayed (turns off plot), Red/Blue, Red/Green, Green/Blue, or ΔE or ΔC (various flavors & reference regions). Red/Blue (the extremes of the spectrum) is the most popular choice for displaying shading. for (plot units). To the right of the Color shading box. Select Pixels (gamma-encoded), Intensity (linear), or f-stop difference. Grayed out if ΔE or ΔC metrics are selected.
- Color uniformity profiles Shows pixel levels along diagonal, vertical, and horizontal lines. The specific display is selected in the dropdown menu on the right. Described below.
- Grid plot Display a grid of results. You can select the grid (m x n) and two parameters to be displayed at each grid location.
- Grid size: single region, 3×3 through 10×10, 20×15, 24×16, 32×18, 15×15,16×16, 20×20, 25×25, 27×27 (not in this exact order).
- Grid calculation:
- Mean (pixel level) and sigma,
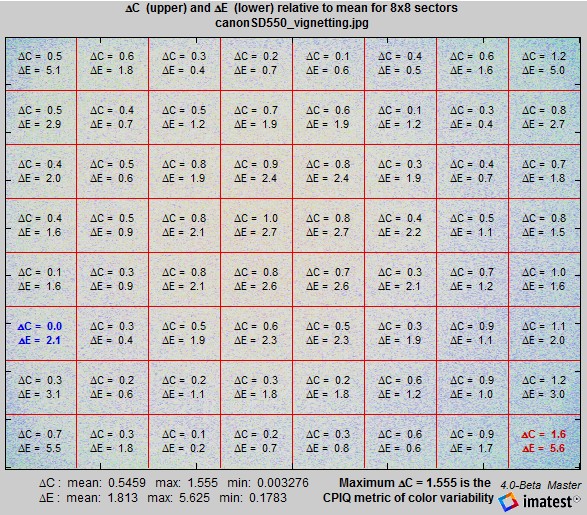
- Color differences Delta-C and Delta-E, Delta-C 94 and Delta-E 94, Delta-C 00 and Delta-E 00,all calculated relative to the mean for the entire image. Note: The CPIQ color variability metric (D) is the maximum Delta-C in the grid plot. It is shown below the plot when Delta-C and Delta-E are selected.
- Mean (pxl) & Delta Color Temp K,
- R/G and B/G pixel ratios,
 CIELAB a* and b*,
CIELAB a* and b*,- Mean (pixel level) and SNR (s/n), Mean (pixel level) and SNR (dB).
- Minimum threshold (0-1) (default = 0). A minimum threshold for pixels to be included in grid plot analysis. Useful for automatically excluding dark areas in images like the one on the right.
We can add more grid plot measurements on request.
- Histogram plot Useful in diagnosing stuck (hot and dead) pixels. Described below.
- Fine detail plot Display a detailed image of noise and sensor nonuniformity (examples below). Slow variations in image density— vignetting (low spatial frequencies) — are removed so that only short to medium range variations— sensor noise, dust spots, etc.— remain. The calculation can be slow and uses lotsof memory because Matlab calculations are performed in double precision mathematics, which requires 24 bytes per color pixel (8 bytes per channel).
Exaggerated local noise (standard) Local noise with added contours Pseudocolor contours with colorbar Spot detection w / threshold (pseudocolor) (Several additional 3D displays) Several display options are available. The first displays noise exaggerated by a factor of 10. The second superposes contour plots (from a smoothed version of the image) on the noisy image. The third produces a pseudocolor image of local nonuniformities (also smoothed) with a color bar (legend) on the right. The fourth emphasizes dark spots, usually caused by dust. A histogram can also be added beneath the fine detail plot.
- Channel You can choose between Red, Blue, Green, or Y (luminance) channels. Color space Used for converting from RGB color space where L*a*b* color difference metrics are displayed.
- Hot and dead pixels By checking the appropriate boxes you can display hot or light pixels (red x) and/or dead or dark pixels (blue •).
 The definition depends on whether Absolute pixel threshold or Relative % threshold is selected:
The definition depends on whether Absolute pixel threshold or Relative % threshold is selected:
Display hot or dead pixels (o): Absolute pixel threshold Hot pixels are stuck at the sensor’s maximum value (255 in 8-bit files) and dead pixels are stuck at 0. Because signal processing— especially JPEG compression— often causes these values to shift, you can use the sliders to set the detection threshold between 6-255 for hot pixels and 0-249 pixels for dead pixels. (The extreme values are for measurements made on white or black fields.) Clicking on or at the ends of the sliders adjusts the threshold by 1. The default values are 252 and 4, respectively. Display light or dark pixels (o): Relative % threshold Light pixels are more than the relative % threshold above the mean of the 8 neighbors; Dark pixels are more than the relative % threshold below the mean of the 8 neighbors. Clusters (in Imatest 4.0+) are defined as groups of two or more adjacent pixels. JPEG files should be saved at the highest quality level for this feature to work well; isolated hot and dead pixels tend to be smudged at lower quality levels. Details of hot and dead pixels are presented below. You can choose whether to count a pixel as hot or dead (light or dark) if the criteria are met by any color channel (the default), all channels, or the selected channel.
Results
Hot and dead pixels (not in Imatest Studio)
of 8185344 total
Threshold: h= 245; d= 10
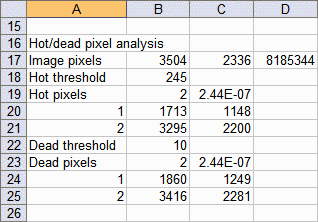
Imatest Master allows you to detect hot and dead pixels. Hot pixels are stuck at or near the sensor’s maximum value (255 in 8-bit files); dead pixels are stuck at or near 0. Image processing (especially demosaicing and data compression) may alter these numbers. Thresholds lower than 255 and higher than 0 are usually required, particularly for JPEG files, where isolated pixels are smeared, even for the highest quality levels. Hot and dead pixels cannot be reliably detected in JPEGs saved at lower quality levels.
The hot and dead pixels shown on the right met the criteria that they were above or below the threshold for any color channel. All channels or the selected channel could have been selected.
The first figure in Uniformity shows two simulated hot (x) and dead (•) pixels. The CSV output file on the right shows the basic statistics for the image (8185344 pixels total). h = 245 and d = 10 are the hot and dead pixel thresholds, respectively. The number and fraction of the hot and dead pixels are shown, followed by the x and y-locations of the first 100 hot and dead pixels. The Histogram plot, described below, is useful for selecting thresholds.
Optical Center
The optical center is the approximate geometric location of the brightest part of the image. It has to be calculated very carefully using a centroid calculation (which is mathematically similar to center of gravity) because noise makes the very broad peak location unreliable— even with highly smoothed images. The horizontal (x) and vertical (y) Optical Centers are calculated separately using the same algorithm. We describe the horizontal calculation.
- Find the mean value (Lmean(x)) of a horizontal band that runs across the image and extends from 0.25 to 0.75 the image height (i.e., half the image height).
- Smooth (lowpass filter) Lmean(x).
- Find the peak value of smoothed Lmean(x). Call it LpeakX. (The peak location is not a stable indicator of the Optical Center.)
- The X-Optical Center is the centroid of the object defined by G(x) = Lmean(x) – 0.95*LpeakX where Lmean(x) > 0.95*LpeakX .
The equation is X-Optical Center = ∫x G(x) dx ⁄ ∫G(x) dx .
Optical center is displayed as a yellow circle (“O”) in luminance contour plots and is reported in the CSV and JSON output files.
Color shading (nonuniformity) (not in Studio)
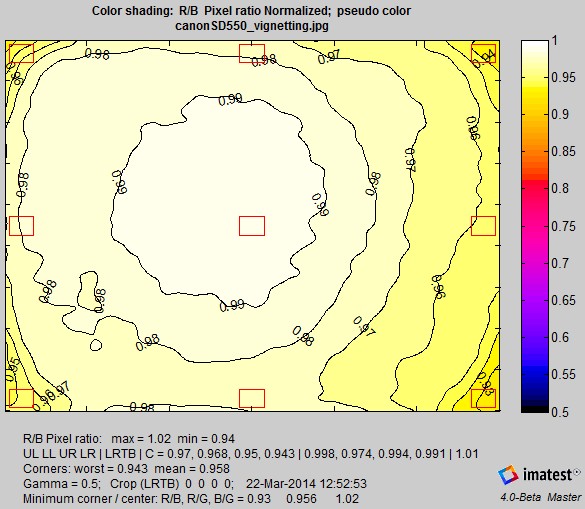
The Color shading plot displays the ratio or difference between R, G, and B channels or L*a*b* color differences (ΔE, ΔC, ΔE94, ΔC94, ΔE00, or ΔC00 ). Two examples are illustrated below. The first shows shading as the ratio of Red to Blue (R/B) channel pixels. Plotted results have been normalized to a maximum of 1.0. Normalization only affects the plots; it makes the plotted results relatively insensitive to white balance errors. The background displays the image with exaggerated colors (HSV saturation S has been increased by 10x for low saturation values; less for high values.)
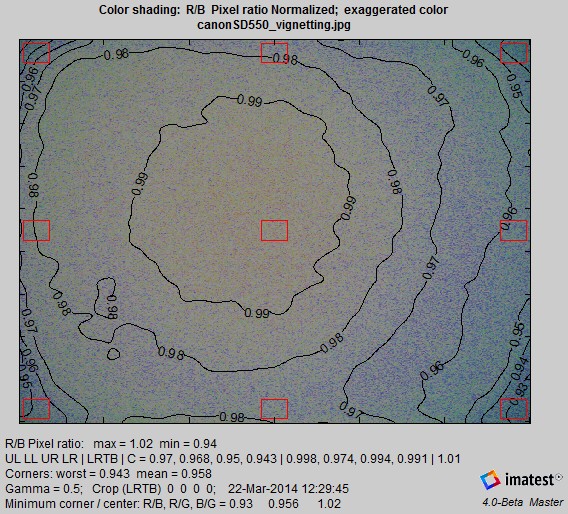 R/B Color shading, exaggerated color.
R/B Color shading, exaggerated color.
Normalization refers to the plot-only. The numbers displayed below the plot are not normalized.
The R/B Pixel ratio max and min (1.02 and 0.94, above (unnormalized)) are taken over the entire smoothed image (not restricted to the corner and side areas indicated by the red rectangles). For this reason they tend to be more extreme than the maxima and minima of the squares (displayed on the next line), and the ratio between them (0.94/1.02 = 0.92) is generally lower than the minimum ratio between the center and the sides & corners. They are calculated and included in numeric outputs (CSV, JSON, and XML files) only when the Color shading plot is produced. Other values (from fixed regions) are always calculated and included in numeric outputs. Two out of twenty-nine of these results are shown in the CSV and JSON examples below.
| Pixel ratios | R/B | R/G | R/B | B/R | G/R | B/G | ||||||||
| Maximum | 1.017 | 1.006 | 1.015 | 1.064 | 1.054 | 1.025 | ||||||||
| Minimum | 0.94 | 0.949 | 0.975 | 0.983 | 0.993 | 0.984 | ||||||||
| Detailed color shading analysis: Imatest 3.7+ | ||||||||||||||
| Result | Center | UL | LL | UR | LR | L-Ctr | R-Ctr | T-Ctr | B-Ctr | Ctr 25% |
Worst corner | Mean corner | Best corner | Pct corner var |
| R/B unnorml | 1.013 | 0.97 | 0.968 | 0.95 | 0.943 | 0.998 | 0.974 | 0.994 | 0.991 | 1.012 | 0.943 | 0.958 | 0.97 | 2.828 |
| R/G unnorml | 1.005 | 0.98 | 0.979 | 0.961 | 0.963 | 0.994 | 0.984 | 0.997 | 0.994 | 1.004 | 0.961 | 0.97 | 0.98 | 1.945 |
JSON output. Values in the image are highlighted.
“pixel_color_stats”: “Pixel ratios, R/B, R/G, R/B, B/R, G/R, B/G,”,
“maximum_stat”: [1.017,1.006,1.015,1.064,1.054,1.025],
“minimum_stat”: [0.9396,0.9487,0.975,0.9829,0.9933,0.9844],
“resTable_comment”: “Results table variables start with resTable_.”,
“resTable_entries”: “Center, UL, LL, UR, LR, L-Ctr, R-Ctr, T-Ctr, B-Ctr, Center 25%,Worst corner, Mean corner, Best corner, Pct corner var”,
“resTable_R_div_B_unnorml”: [1.0134,0.9702,0.96837,0.95031,0.94276,0.99793,0.97397,0.99369,0.99091,1.0124,0.94276,0.95791,0.9702,2.828],
“resTable_R_div_G_unnorml”: [1.0047,0.97956,0.97873,0.9605,0.96265,0.99398,0.98409,0.99673,0.99411,1.0043,0.9605,0.97036,0.97956,1.945],
The second example shows the R/B ratio in pseudocolor. (The difference in f-stops could also be displayed, but is not shown here.) Plotted results have been normalized to 1.0.
 R/B color shading, pseudocolor.
R/B color shading, pseudocolor.
Color nonuniformity can be displayed as one of the L*a*b* color difference metrics (ΔE = sqrt(ΔL*2 + Δa*2 + Δb*2 ), ΔC = sqrt(Δa*2 + Δb*2 ), ΔE94, ΔC94, ΔE00, ΔC00 ), referred to the center of the image (either the central region, with size specified in the Corner and side regions box or the central 25% by area). The ΔC metrics are of particular interest for color metrics because they omit luminance differences (ΔL*). It is displayed below as a 3D plot, which can be rotated for enhanced visualization..
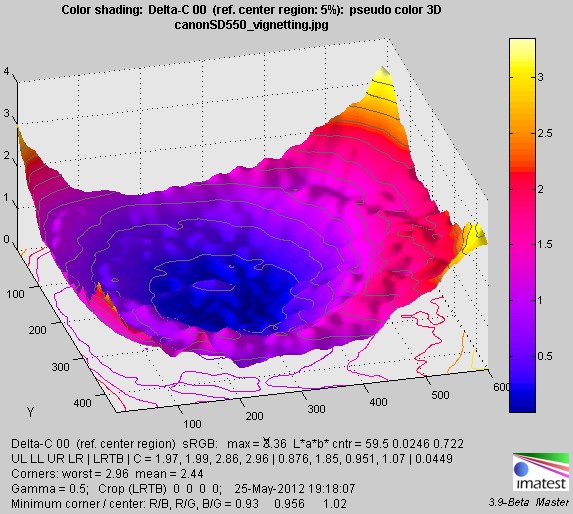
ΔC 2000 color shading (omits ΔL*), 3D shaded pseudocolor.
The Extra smoothing box should always be checked for 3D plots.
Uniformity profiles (not in Studio)
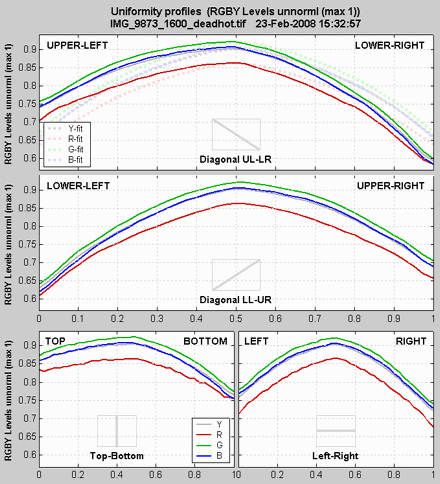
Uniformity profiles.Uniformity profiles displays profiles of image levels along several lines: Diagonal Upper Left-Lower Right, Diagonal Lower Left-Upper Right, Vertical Top-Bottom (center), and Horizontal Left-Right (center). Several display options are listed below.
| RGBY unnormalized (max 1) |
| RGBY unnormalized pixels (max 255) |
| RGBY normalized (max 1) |
| Ratios: R/G, B/G (G constant) |
| RGBY normalized: ALL CHANNELS |
| Delta L* a* b* C* (C* = chroma) |
The independent axis goes from 0 to 1 in steps of 0.025 (41 steps total). Detailed results for the 41 steps are written to the CSV and XML output files.
Polynomial fit A fourth order fit to R, G, B, and Y (or L*, a* and b*) is shown as faint dotted lines in the upper (Diagonal UL-LR) plot. The equation for the fit is
y = c1r4 + c2r3 + c3r2 + c4r + c4
where r is the distance from the center normalized to the center-to-corner distance (r = 1 at the corners). The R, G, B, and Y coefficients are in displayed the CSV and XML output files. There is not enough space to show them in the plot. They have the following format in the CSV output file.
|
Fourth order fit: y = c(1)*r^4 + C(2)*r^3 + … + c(5) where r is normalized to center-to-corner. |
|||||
| R | 0.045 | -0.108 | -0.081 | -0.083 | 0.866 |
| G | -0.124 | 0.207 | -0.295 | -0.037 | 0.922 |
| B | -0.189 | 0.315 | -0.341 | -0.037 | 0.907 |
Grid plot
Several grid choices (3×3 through 32×18) and plot calculations are available.
For the grid plot, which implements the CPIQ Phase 2 specification, the mean of the entire image is used as the reference for calculating ΔC and ΔE.
Histograms (not in Studio)
The histogram plot, introduced in Imatest Master 2.3.11 (July 2007), facilitates the detection and the setting of thresholds for stuck (hot, dead, etc.) pixels. Histograms of log10(occurrences+1) are displayed for the red, green, and blue channels. [The logarithm compresses the plot so even a single bad pixel is visible. log10(occurrences+1) is used because log(0) = −∞ (minus infinity), while log(1) = 0.]
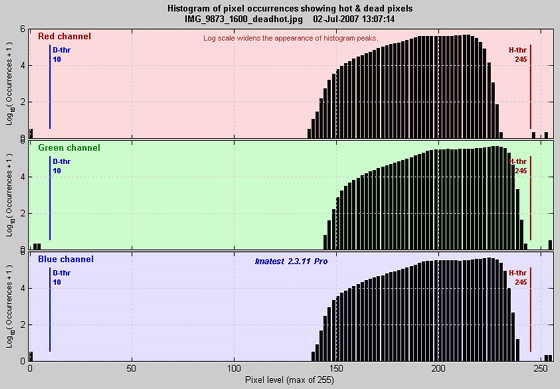
R, G, and B Histograms showing stuck pixels.
In this example, single stuck pixels are plainly visible near levels 0 and 252. Altough these stuck pixels were synthesized, their levels is slightly different due to JPEG compression (they were the same in a TIFF file). The dead pixel threshold is shown on the left in blue; the hot pixel threshold is shown on the right in red. You can quickly see if the thresholds are set correctly— if they are outside the valid density region and if the dead and hot pixels are above and below their respective thresholds. You can change threshold settings and rerun Uniformity if necessary.
Noise detail (not in Studio)
shows an exaggerated or pseudocolor image of the noise detail with long-range density variations removed. Four options are available:
| Exaggerated local noise (standard)
|
Exaggerated image of local noise |
| Local noise with added contours | Exaggerated image of local noise with added contours |
| Pseudocolor contours with colorbar | Pseudocolor image of local density variations. The image has been smoothed. Colors vary from image to image: the color map covers the density range of the image. |
| Spot detection w / threshold (pseudocolor) | Pseudocolor image emphasizing spots. Fixed color map. Image is normalized to the mean density. For clarity, only densities between 0.9 and 1 are displayed in the color map. |
| 3D Pseudocolor Contours shaded | 3D pseudocolor image may be rotated for enhanced visualization. Shading emphasizes contour shapes. |
| 3D Pseudocolor Contours | The Colormap (which relates color to levels) is more accurate without shading. |
| 3D Inverted Pseudocolor Contours shaded | Inverts the data (Z-axis) |
| 3D Inverted Pseudocolor Contours | |
| 3D Spot detection, pseudocolor shaded | 3D spot detection. The Z-axis is always inverted so spots stand out. |
| 3D Spot detection, pseudocolor |
The local noise figures are produced by
- Subtracting a highly smoothed version of the image from the image itself. This removes broad image variations (low spatial frequencies), leaving only the fine detail. (The signal is highpass filtered.) Exaggerating the fine detail by a factor 5x or 10x, depending on the signal-to-noise ratio (the average pixel level of the original image divided by the standard deviation of the difference image (the results of step 1), i.e., the RMS noise). Adding an offset to the the exaggerated signal so the average level of the image is displayed as middle gray.
- If Local noise with added contours is selected, contours are calculated by subtracting the same highly smoothed version of the image from a moderately smoothed version of the image. Smoothing is necessarily because noise would make the contours unintelligibly rough.
The first image (below) shows noise detail for the Canon EOS-20D at ISO 1600 with the 10-22mm lens set to f/4.5. No surprises here; electronic noise dominates.
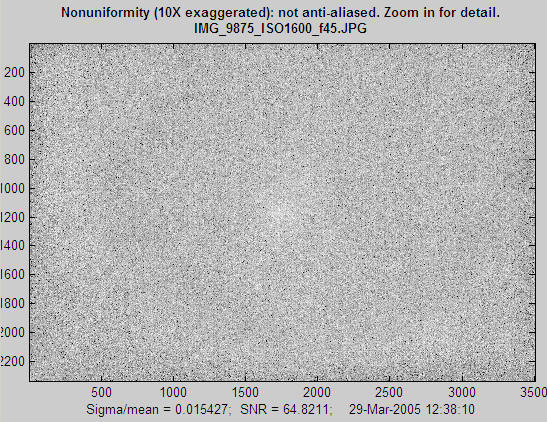
Noise detail for Canon EOS-20D, ISO 1600, 10-22mm lens, f/4.5.
The second image (below) shows noise detail for the Canon EOS-20D at ISO 100 with the 10-22mm lens set to f/8. Thanks to the small aperture, some very faint dust spots are visible. The dust is on the anti-aliasing/infrared filter/microlens assembly in front of the sensor. This assembly can be well over 1 millimeter thick. Stopping the lens down (increasing the f-stop setting) reduces the size of dust spots but makes them darker. This image has a surprise in the form of concentric circles: bands where the noise appears to be higher or lower than the remainder of the image. This may be caused by (a) the Analog-to-Digital (A-D) converter in the image sensor chip, which can have small discontinuities when, for example going from level 127 to 128: binary 01111111 to 10000000, or (b) JPEG artifacts. Rrecall that these noniniformities are exaggerated by a factor of 10: they would be invisible or barely visible on an actual image; you might seem then faintly in smooth areas like skies.

Noise detail, Canon EOS-20D, ISO 100, 10-22mm lens, f/8.
Here is the same image, displayed in pseudocolor (which shows the amount of variation) with a color bar, and including a histogram (of individual pixels, not the smoothed image used to generate the contour plot on the left). The scale varies from image to image; it is not fixed like the scales for for the luminance and f-stop contour plots (which display long range, low spatial frequency variations). The histogram is narrower than the separate histogram image (above) because long-range (low spatial frequency) density variations have been removed. It is a good approximation to the average sensor noise. The circular pattern may originate with reflections between the light source, lens, and sensor.
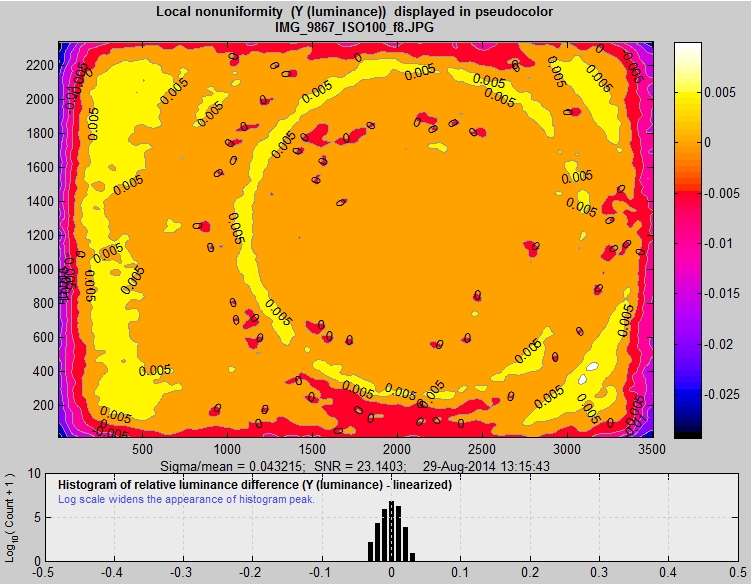 Local nonuniformities shown in pseudocolor, Canon EOS-20D, ISO 100, 10-22mm lens, f/8.
Local nonuniformities shown in pseudocolor, Canon EOS-20D, ISO 100, 10-22mm lens, f/8.
The image below is an enlargement (a zoom) of the above image, centered on the dust spot to the left of the center. You can zoom into an image by using the mouse to draw an rectangle, or by simply clicking on a feature you want to enlarge. You can restore the original image by double-clicking anywhere on the image.
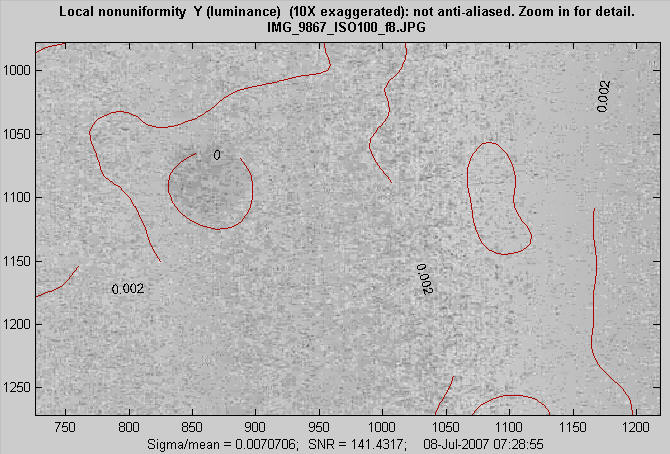
The following image is the noise detail from a 2 f-stop underexposed image with maximum luminance = 0.161 (out of 1), f/4.5, ISO 100. It shows a clear pattern. Although it looks alarming, this pattern is invisible because (a) it is in a very dark region, (b) it is aliased. The actual pattern has a much higher spatial frequency, hence is less visible. You need to zoom in to view the true pattern, which is less visible than it appears here.
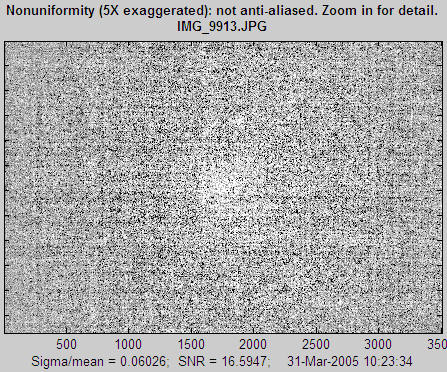
Noise detail, illustrating aliasing. (The actual noise is not as bad as it looks.)
Spot detection (not in Studio; better with Blemish Detect)
| Note: Spot detection is handled with much more detail and greater accuracy in Blemish Detect, which allows the spot filtering and thresholds to be tuned to viewing conditions based on an understanding of the human eye. |
When Spot detection w / threshold (pseudocolor) is selected in the Noise detail popup menu, the pseudocolor display emphasizes dark spots (the type that result from dust on the sensor) and minimizes noise, light spots, and long range density variations. The following webcam image (originally 1600 pixels wide) has two rows of five simulated spots (added by an image editor). Other irregularities are from the sensor itself.

Webcam image with 10 simulated spots (5 in each of 2 rows)
With the standard Pseudocolor contours with colorbar display, the darker spots are clearly visible, but the lighter spots are lost in the overall density variations.
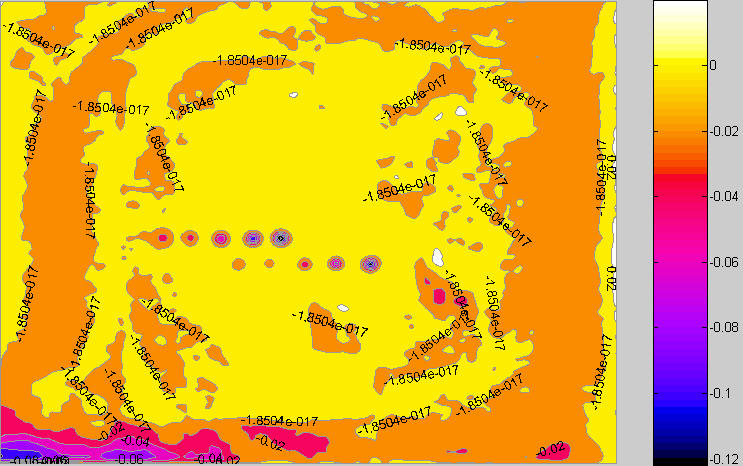
Image with spots: standard pseudocolor display
But they stand out in the Spot detection display. The differences in the algorithms are described below.
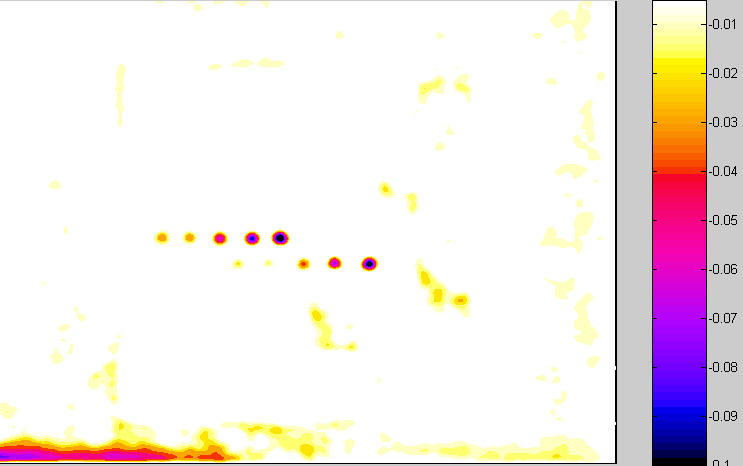
Image with spots: Spot detection display
When Pseudocolor contours with colorbar is selected, the image is normalized to its average level. Then the local variations are calculated by subtracting a highly smoothed version of the image from a moderately smoothed version of the image. This is the same data used for the contours in the Local noise with added contours display, described above. When Spot detection w / threshold (pseudocolor) is selected, there are several differences.
- The “highly” smoothed version of the image is less aggressively smoothed. This emphasizes local variations more strongly.
- The contour plot has a fixed color map, showing only values between = -0.005 (-0.5%), which is about the threshold of visibility for a spot, and -0.1 (-10%), which is the density for a highly visible spot. All values above -0.005 are displayed as white and all values below -0.1 are displayed as black. The color map for the standard pseudocolor plot is variable, based on the minimum and maximum values of the processed image.
This approach removes much of the interfering detail from the final plot so that spots are clearly visible.

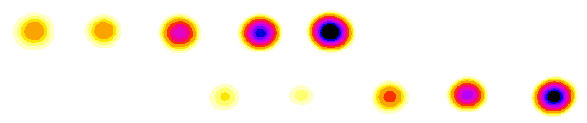
Detail: Simulated spots and Spot detection display
|
Fourth order fit: y = c(1)*r^4 + C(2)*r^3 + … + c(5) where r is normalized to center-to-corner. |
|||||
| R | 0.045 | -0.108 | -0.081 | -0.083 | 0.866 |
| G | -0.124 | 0.207 | -0.295 | -0.037 | 0.922 |
| B | -0.189 | 0.315 | -0.341 | -0.037 | 0.907 |
Hot and dead pixels By checking the appropriate boxes you can display hot or light pixels (red x) and/or dead or dark pixels (blue •).
 The definition depends on whether Absolute pixel threshold or Relative % threshold is selected:
The definition depends on whether Absolute pixel threshold or Relative % threshold is selected:
| Pixel ratios | R/B | R/G | R/B | B/R | G/R | B/G | ||||||||
| Maximum | 1.017 | 1.006 | 1.015 | 1.064 | 1.054 | 1.025 | ||||||||
| Minimum | 0.94 | 0.949 | 0.975 | 0.983 | 0.993 | 0.984 | ||||||||
| Detailed color shading analysis: Imatest 3.7+ | ||||||||||||||
| Result | Center | UL | LL | UR | LR | L-Ctr | R-Ctr | T-Ctr | B-Ctr | Center 25% | Worst corner | Mean corner | Best corner | Pct corner var |
| R/B unnorml | 1.013 | 0.97 | 0.968 | 0.95 | 0.943 | 0.998 | 0.974 | 0.994 | 0.991 | 1.012 | 0.943 | 0.958 | 0.97 | 2.828 |
| R/G unnorml | 1.005 | 0.98 | 0.979 | 0.961 | 0.963 | 0.994 | 0.984 | 0.997 | 0.994 | 1.004 | 0.961 | 0.97 | 0.98 | 1.945 |
| B/G unnorml | 0.991 | 1.009 | 1.01 | 1.011 | 1.021 | 0.996 | 1.01 | 1.003 | 1.003 | 0.992 | 1.009 | 1.013 | 1.021 | 1.122 |